题目内容
4.当x2-4x+1=0时,求$\frac{{x}^{2}}{1-x}$+1+$\frac{1}{{x}^{2}-x}$的值.分析 先将$\frac{{x}^{2}}{1-x}$+1+$\frac{1}{{x}^{2}-x}$化简为:-$\frac{{x}^{2}+x+1}{x}$+1,然后根据x2-4x+1=0,求出x2+x+1=5x,然后代入求解即可.
解答 解:$\frac{{x}^{2}}{1-x}$+1+$\frac{1}{{x}^{2}-x}$
=$\frac{{x}^{2}}{1-x}$+1-$\frac{1}{x(1-x)}$
=$\frac{{x}^{3}}{x(1-x)}$-$\frac{1}{x(1-x)}$+1
=$\frac{{x}^{3}-1}{x(1-x)}$+1
=$\frac{(x-1)({x}^{2}+x+1)}{x(1-x)}$+1
=-$\frac{{x}^{2}+x+1}{x}$+1
∵x2-4x+1=0
∴x2+1=4x,
∴x2+x+1=5x,
∴原式=-$\frac{{x}^{2}+x+1}{x}$+1=-$\frac{5x}{x}$+1=-5+1=-4.
点评 本题考查了分式的化简求值,解答本题的关键在于将$\frac{{x}^{2}}{1-x}$+1+$\frac{1}{{x}^{2}-x}$化简为:-$\frac{{x}^{2}+x+1}{x}$+1,然后根据x2-4x+1=0,求出x2+x+1=5x,然后代入求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.有理数a、b、c的大小关系如图,则下列关系式中:①a+b+c>0;②|a+b|<c;③|a-c|=|a|+c;④|b-c|>|c-a|,其中一定成立的是( )
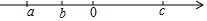
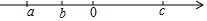
| A. | ②③ | B. | ①④ | C. | 只有③ | D. | ②③④ |
15.一个正数的两个平方根分别是2m-1和4-3m,则m的值是( )
| A. | -5 | B. | 3 | C. | 5 | D. | 25 |
9.若a是一位数,b是两位数,把a放在b的左边,所得的三位数可以表示为( )
| A. | 10a+b | B. | 10b+a | C. | 100a+b | D. | ab |
 如图,把直线y=-2x向上平移后得到直线AB,直线AB 经过点(m,n),且2m+n=6,直线AB的关系式是y=-2x+6.
如图,把直线y=-2x向上平移后得到直线AB,直线AB 经过点(m,n),且2m+n=6,直线AB的关系式是y=-2x+6. 如图,点P是菱形ABCD的对角线DB延长线上一点,连接PC并延长,交AD延长线于点E,AB延长线于点F.
如图,点P是菱形ABCD的对角线DB延长线上一点,连接PC并延长,交AD延长线于点E,AB延长线于点F.