题目内容
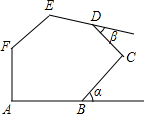 如图,在六边形ABCDEF中,AB⊥AF,BC⊥DC,∠E+∠F=260°,求两外角和∠α+∠β的度数.
如图,在六边形ABCDEF中,AB⊥AF,BC⊥DC,∠E+∠F=260°,求两外角和∠α+∠β的度数.
解:∵AB⊥AF,BC⊥DC,
∴∠A+∠C=90°,
∵∠E+∠F=260°,
∴∠EDC+∠ABC=(6-2)×180°-90°×2-260°=280°,
∴∠α+∠β=360°-(∠EDC+∠ABC)=80°.
故两外角和∠α+∠β的度数为80°.
分析:先根据垂直的定义和多边形内角和定理得到∠EDC+∠ABC的度数,再根据多边形内角与外角的关系即可求解.
点评:考查了垂直的定义和多边形内角和定理多边形内角与外角的关系,注意整体思想的运用.
∴∠A+∠C=90°,
∵∠E+∠F=260°,
∴∠EDC+∠ABC=(6-2)×180°-90°×2-260°=280°,
∴∠α+∠β=360°-(∠EDC+∠ABC)=80°.
故两外角和∠α+∠β的度数为80°.
分析:先根据垂直的定义和多边形内角和定理得到∠EDC+∠ABC的度数,再根据多边形内角与外角的关系即可求解.
点评:考查了垂直的定义和多边形内角和定理多边形内角与外角的关系,注意整体思想的运用.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
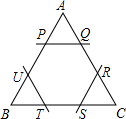 如图所示,△ABC是边长为a的正三角形纸张,今在各角剪去一个三角形,使得剩下的六边形PQRSTU为正六边形,则此正六边形的周长为何( )
如图所示,△ABC是边长为a的正三角形纸张,今在各角剪去一个三角形,使得剩下的六边形PQRSTU为正六边形,则此正六边形的周长为何( )| A、2a | ||
| B、3a | ||
C、
| ||
D、
|
 23、如图,在六边形ABCDEF中,AB=BC=CD=DE=EF=FA,∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,对角线AE与BF相交于点M,BD与CE相交于点N.
23、如图,在六边形ABCDEF中,AB=BC=CD=DE=EF=FA,∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,对角线AE与BF相交于点M,BD与CE相交于点N.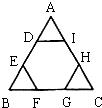 18、如图,正六边形DEFGHI的顶点都在边长为6cm的正三角形ABC的边上,则这个正六边形的边长是
18、如图,正六边形DEFGHI的顶点都在边长为6cm的正三角形ABC的边上,则这个正六边形的边长是 如图,在六边形ABCDEF中,BA⊥FA,BC⊥DC,∠α、∠β分别是∠ABC和∠EDC的补角,∠α=55°,∠β=30°,则∠E+∠F的度数为
如图,在六边形ABCDEF中,BA⊥FA,BC⊥DC,∠α、∠β分别是∠ABC和∠EDC的补角,∠α=55°,∠β=30°,则∠E+∠F的度数为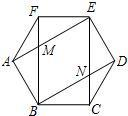 如图,在六边形ABCDEF中,AB=BC=CD=DE=EF=FA,∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,对角线AE与BF相交于点M,BD与CE相交于点N.
如图,在六边形ABCDEF中,AB=BC=CD=DE=EF=FA,∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,对角线AE与BF相交于点M,BD与CE相交于点N.