题目内容
20．甲乙两地相距380km，一辆贩毒车从甲地赶往乙地接头取货，警方截取情报后立即组织干警从甲地出发赶往乙地缉拿这伙犯罪分子，结果警车与贩毒车同时到达，警方迅速将犯罪分子一网打尽，已知贩毒车比警车早出发1$\frac{1}{4}$h，警车与贩毒车的速度比为4：3，求警车和贩毒车的速度？分析 设长途汽车的速度为xkm/小时，则小汽车的速度为3xkm/小时，根据警车与贩毒车之间的时间关系建立方程求出其解，即可得出结果．
解答 解：设警车的速度为4xkm/h，则贩毒车的速度为3xkm/h，
根据题意得：$\frac{380}{4x}+\frac{5}{4}=\frac{380}{3x}$，
解得：x=$\frac{76}{3}$，
经检验，x=$\frac{76}{3}$是原方程的根，
∴原方程的根为x=$\frac{76}{3}$．
∴警车的速度为：4×$\frac{76}{3}$=$\frac{304}{3}$（km/h），贩毒车的速度为：3×$\frac{76}{3}$=76（km/h）．
答：警车的速度为$\frac{304}{3}$km/h，贩毒车的速度为76km/h．
点评 本题是一道行程问题的运用题，考查了列分式方程解实际问题的运用、分式方程的解法；根据题意列出方程是解决问题的关键，注意检验．
练习册系列答案
相关题目
如图，在离旗杆30m的A处，用测角仪测得旗杆顶端D的仰角为30°，测得旗杆底部C的俯角为α，且tanα=$\frac{1}{30}$，试求：
11．某保险公司推出如下的重大疾病险，根据病人的情况报销一定比例的医疗费．医疗费的报销比例标准如下表：
（1）某人在医院实际医疗费为8000元．请问能报销多少钱？
（2）若此人某次住院的自付医疗费为2600元（自付医疗费=实际医疗费-按标准报销的金额），则此人此次住院的实际医疗费为多少元？
| 费用范围 | 500元以下（含500元） | 超过500元且不超过10000元的部分 | 超过10000元的 部分 |
| 报销标准 | 不予报销 | 70% | 80% |
（2）若此人某次住院的自付医疗费为2600元（自付医疗费=实际医疗费-按标准报销的金额），则此人此次住院的实际医疗费为多少元？
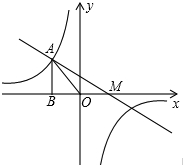如图，点A（-2，b）是函数y=$\frac{k}{x}$的图象上的点，过点A作AB⊥x轴于点B，△AOB的面积为2，若一次函数y=ax+1的图象经过点A且与x轴交于点M，则AO：AM=$\sqrt{2}$：$\sqrt{5}$．