题目内容
甲、乙、丙三名学生要从A、B两个社区中随机选取一个参加社会实践活动.
(1)求甲、乙、丙三名学生在同一个社区参加社会实践活动的概率;
(2)求甲、乙、丙三名学生至少有两人在A社区参加社会实践活动的概率.
解:可能出现的结果
(1)由上表可知,可能的结果共有8种,且他们都是等可能的,其中,甲、乙、丙三名学生在同一个社区参加社会实践活动的结果有2种,
则所求概率P1=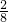 =
= ;
;
(2)甲、乙、丙三名学生至少有两人在A社区参加社会实践活动的结果有4种,
则所求概率P2=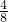 =
= .
.
分析:列表得出所有等可能的情况数,
(1)找出甲、乙、丙三名学生在同一个社区参加社会实践活动的情况数,即可求出所求的概率;
(2)找出甲、乙、丙三名学生至少有两人在A社区参加社会实践活动的情况数,即可求出所求的概率.
点评:此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.
| 甲 | 乙 | 丙 | 结果 |
| A | A | A | (A,A,A) |
| A | A | B | (A,A,B) |
| A | B | A | (A,B,A) |
| A | B | B | (A,B,B) |
| B | A | A | (B,A,A) |
| B | A | B | (B,A,B) |
| B | B | A | (B,B,A) |
| B | B | B | (B,B,B) |
则所求概率P1=
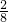 =
= ;
;(2)甲、乙、丙三名学生至少有两人在A社区参加社会实践活动的结果有4种,
则所求概率P2=
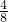 =
= .
.分析:列表得出所有等可能的情况数,
(1)找出甲、乙、丙三名学生在同一个社区参加社会实践活动的情况数,即可求出所求的概率;
(2)找出甲、乙、丙三名学生至少有两人在A社区参加社会实践活动的情况数,即可求出所求的概率.
点评:此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
某班要从甲、乙、丙三名候选人中选出一名参加学校组织的知识竞赛.班上对三名候选人进行了笔试和口试两次测试,测试成绩如下表:
班上50名学生又对这三名候选人进行了民主投票,三人的得票率(没有弃权票,每位学生只能投三人中的一票)如下图,每得一票记1分.
(1)请分别算出三人的得票分;
(2)如果根据三项得分的平均成绩高者被当选,那么谁将被当选?(精确到0.01)
(3)如果根据笔试、口试、投票三项成绩按5:3:2的比例确定成绩,根据成绩的加权平均数高者当选,那么谁又将被当选?

| 测试项目 | 测试成绩 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 70 | 80 | 85 |
| 口试 | 90 | 70 | 65 |
(1)请分别算出三人的得票分;
(2)如果根据三项得分的平均成绩高者被当选,那么谁将被当选?(精确到0.01)
(3)如果根据笔试、口试、投票三项成绩按5:3:2的比例确定成绩,根据成绩的加权平均数高者当选,那么谁又将被当选?
