题目内容
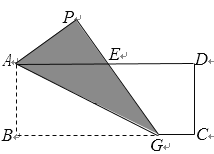
【题目】如图,![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转得
逆时针旋转得![]() ,当点
,当点![]() 落在
落在![]() 上时,
上时,![]() ,则阴影部分的面积为____.
,则阴影部分的面积为____.
【答案】![]()
【解析】
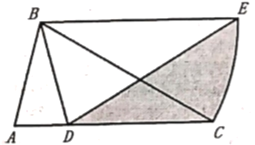
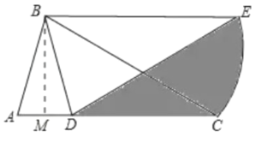
根据等腰三角形的性质和旋转的性质求得∠CBE=ABD=30°,根据平行线的性质求得∠ACB=∠CBE=30°,进而求得AB=AC=6,解直角三角形求得BM、MC,即可求得AD,由图形可知阴影部分的面积=△BDC的面积+扇形BCE的面积△ABC的面积,根据扇形面积公式和三角形面积公式计算即可.
解:∵∠A=75°,AB=AD,
∴∠ADB=∠A=75°,
∴∠ABD=180°2×75°=30°,
∴∠CBE=ABD=30°,
∵BE∥AC,
∴∠ACB=∠CBE=30°,
∴∠ABC=75°,
∴BC=AC=6,
作BM⊥AC于M,则AM=DM,
∴BM=![]() BC=3,MC=
BC=3,MC=![]() BC=3
BC=3![]() ,
,
∴AM=AC=MC=63![]() ,
,
∴AD=126![]() ,
,
由图形可知,阴影部分的面积=△BDC的面积+扇形BCE的面积△ABC的面积,
∴阴影部分的面积
=扇形BCE的面积△ABD的面积
=![]()
=![]() ,
,
故答案为: ![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目