Question

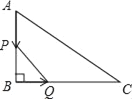
【题目】如图，在△ABC中，∠B=90°，BC=8cm，AC=10cm，动点A从点A出发以1cm/s的速度沿AB边运动，同时动点Q从点B出发以2cm/s的速度沿BC边运动．设运动时间为t秒．

（1）若△PBQ的面积等于8cm2，求t的值；

（2）若PQ的长等于cm，求t的值．

Answer 1

【答案】（1）当P、Q经过2或4秒时，△PBQ的面积为8cm2；（2）当t为1或时，PQ的长等于cm．

【解析】分析：（1）由题意，利用勾股定理求得AB=6，可设P、Q经过t秒，使△PBQ的面积为8cm2，则PB=6﹣t，BQ=2t，根据三角形面积的计算公式，S△PBQ=BQPB，列出方程，解答出即可；

（2）可设P、Q两点运动t秒时，则PB=6﹣t，BQ=2t，根据勾股定理，可得PQ2=BP2+BQ2，代入整理即可求出．

详解：（1）AB==6，设P、Q经过t秒时，△PBQ的面积为8cm2，则PB=6﹣t，BQ=2t．

∵∠B=90°，AB=6cm，BC=8cm，∴，（6﹣t）2t=8，解得：t1=2，t2=4．

答：当P、Q经过2或4秒时，△PBQ的面积为8cm2；

（2）设P、Q两点运动t秒时，PQ的长等于cm，则29=（6﹣t）2+（2t）2，解得：t1=1，t2=．

答：当t为1或时，PQ的长等于cm．