题目内容
【题目】已知直线l
经过A（2，3）B（
，0）
(1) 求直线l的解析式及l与坐标轴围成的图形的面积.
(2) 将l向下平移3个单位长度，再向左平移1个单位长度，得到直线l
，画出l的图象并直接写出l的解析式__________________.
(3)若点M（
，m），N（n，1）在直线l上，P为y轴上一动点，则PM+PN最小时，P的坐标为____________，此时PM+PN=______________.
【答案】（1）y=6x-9，
；（2）y=6x-6；（3）P（0，
），
.
【解析】
（1）已知A，B点坐标，利用待定系数法求直线l
的解析式，根据解析式求出直线l与坐标轴的交点，然后计算面积即可；
（2）先画出l的图象，然后向下平移3个单位长度，再向左平移1个单位长度画出l
的图象，根据一次函数图象平移的规律得出l的解析式；
（3）求出M，N坐标，作点N关于y轴的对称点N’，连接MN’交y轴于点P，则此时PM+PN最小，然后用待定系数法求出直线MN’的解析式可得P的坐标，用两点间距离公式可求出PM+PN的长.
解：（1）设直线l的解析式为：y=kx+b(k≠0)，
将点A（2，3）B（
，0）代入可得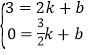
，
解得：
，
∴直线l的解析式为：y=6x-9，
当x=0时，y=-9，当y=0时，x=，
∴与坐标轴围成的图形的面积=
；
（2）l的图象如图所示：
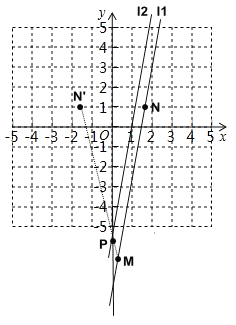
根据一次函数图象平移的规律可得l的解析式为：y=6x-6；
（3）将M（
，m），N（n，1）分别代入y=6x-9，
可得m=
，n=
，
∴M（，），N（，1），
作点N关于y轴的对称点N’，连接MN’交y轴于点P，
则此时PM+PN最小，且N’（
，1）
设直线MN’解析式为：y1=k1x+b1(k≠0)，
将M（，），N’（，1）代入可得：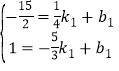
，
解得：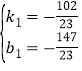
，
∴直线MN’解析式为：y1=
x，
∴P的坐标为（0，），此时PM+PN=
.
