Question

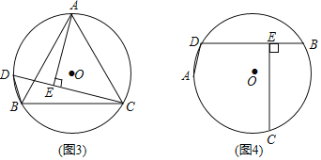
【题目】如图，在Rt△ABC中，∠ACB＝90°．

（1）以AB边上一点O为圆心作⊙O，使⊙O经过点A，C；（保留作图痕迹，不写作法）

（2）判断点B与⊙O的位置关系是　 　．（直接写出答案）

Answer 1

【答案】（1）见解析；（2）点B在⊙O上，理由见解析

【解析】

（1）作线段AC的垂直平分线EF交AB于点O，以O为圆心，OA为半径作⊙O，⊙O即为所求．

（2）根据OA＝OC＝OB即可判断．

解：（1）如图，⊙O即为所求．

（2）点B在⊙O上．

理由：∵EF垂直平分线段AC，

∴OA＝OC，

∴∠OAC＝∠OCA，

∵∠OAC+∠B＝90°，∠OCA+∠BCO＝90°，

∴∠OCB＝∠OBC，

∴OC＝OB，

∴OA＝OC＝OB，

∴点B在⊙O上．

故答案为点B在⊙O上．