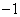题目内容
如图,已知在△ABC中,DE∥BC,EF∥AB,AE=2CE,AB=6,BC=9.求:
(1)求BF和BD的长度.
(2)四边形BDEF的周长.

【考点】平行线分线段成比例;平行四边形的判定与性质.
【分析】(1)由平行线分线段成比例得出比例式,即可得出结果;
(2)先证明四边形BDEF是平行四边形,得出对应边相等,即可得出结果.
【解答】解:(1)∵AE=2CE,
∴ ,
,
∵EF∥AB
∴ ,
,
∵BC=9,
∴BF=6,
∵DE∥BC
∴ ,
,
∵AB=6,
∴BD=2;
(2)∵EF∥AB,DE∥BC
∴四边形BDEF是平行四边形,
∴BD=EF=2,DE=BF=6,
∴四边形BDEF的周长2(2+6)=16.
【点评】本题主要考查平行线分线段成比例;掌握平行线分线段中的线段对应成比例是解题的关键,注意线段的对应关系.

练习册系列答案
相关题目
数轴上三个点表示的数分别为p、r、s.若p-r =5,s-p=2,则s-r等于( )
| A.3 | B.﹣3 | C.7 | D.﹣7 |
下列交通标志中,既是轴对称图形又是中心对称图形的是
|
|
|
|
| |
| A | B | C | D |
 .
.





 ,且0°<
,且0°<


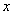 的方程
的方程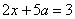 的解与方程
的解与方程 的解相同,则
的解相同,则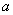 的值是
的值是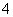 B.
B.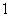 C.
C.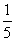 D.
D.