题目内容
5.一只不透明的袋子中装有2个白球和1个红球,这些球除颜色外都相同,搅匀后从中任意摸出1个球(不放回),再从余下的2个球中任意摸出1个球.(1)用树状图或列表等方法列出所有可能出现的结果;
(2)求两次摸到的球的颜色不同的概率.
分析 (1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;
(2)由(1)中树状图可求得两次摸到的球的颜色不同的情况有4种,再利用概率公式求解即可求得答案.
解答 解:(1)如图: ;
;
(2)共有6种情况,两次摸到的球的颜色不同的情况有4种,概率为$\frac{4}{6}$=$\frac{2}{3}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.抛物线y=2(x-3)2+4顶点坐标是( )
| A. | (3,4) | B. | (-3,4) | C. | (3,-4) | D. | (2,4) |
13. 如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )
如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )
 如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )
如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )| A. | $3\sqrt{3}$ | B. | 6 | C. | 4 | D. | 5 |
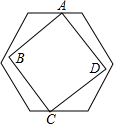 如图,有一个边长不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组平行的对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是$\frac{\sqrt{6}}{2}$≤a≤3-$\sqrt{3}$.
如图,有一个边长不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组平行的对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是$\frac{\sqrt{6}}{2}$≤a≤3-$\sqrt{3}$. 如图,在圆内接四边形ABCD中,若∠A,∠B,∠C的度数之比为4:3:5,则∠D的度数是120°.
如图,在圆内接四边形ABCD中,若∠A,∠B,∠C的度数之比为4:3:5,则∠D的度数是120°.


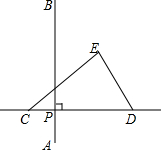 如图,在平面内,线段AB=6,P为线段AB上的动点,三角形纸片CDE的边CD所在的直线与线段AB垂直相交于点P,且满足PC=PA.若点P沿AB方向从点A运动到点B,则点E运动的路径长为6$\sqrt{2}$.
如图,在平面内,线段AB=6,P为线段AB上的动点,三角形纸片CDE的边CD所在的直线与线段AB垂直相交于点P,且满足PC=PA.若点P沿AB方向从点A运动到点B,则点E运动的路径长为6$\sqrt{2}$.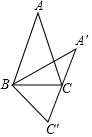 如图,在△ABC中,AB=AC,将△ABC绕顶点B顺时针旋转,得到△A′BC′.设∠A=α,当A′C′恰好经过顶点C时,∠A′BC=90°-$\frac{3α}{2}$(用含α的式子表示).
如图,在△ABC中,AB=AC,将△ABC绕顶点B顺时针旋转,得到△A′BC′.设∠A=α,当A′C′恰好经过顶点C时,∠A′BC=90°-$\frac{3α}{2}$(用含α的式子表示).