Question

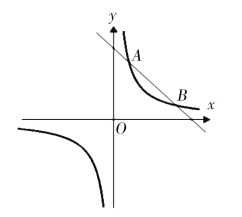
【题目】已知抛物线G：y=x2-2mx与直线l：y=3x+b相交于A，B两点（点A的横坐标小于点B的横坐标）

（1）求抛物线y=x2-2mx顶点的坐标（用含m的式子表示）；

（2）已知点C(-2，1)，若直线l经过抛物线G的顶点，求△ABC面积的最小值；

（3）若平移直线l,可以使A，B两点都落在x轴的下方，求实数m的取值范围．

Answer 1

【答案】（1）；（2）；（3）m＞3或m＜-3

【解析】

（1）将抛物线解析式化为顶点式即可求解；

（2）根据直线过抛物线顶点，可以将顶点坐标代入解析式求出b，之后联立方程求出A、B两点的坐标；过C点做CD∥y轴交直线于D，可以发现C在D的上方，并且不论CD在A、B左侧、中间还是右侧，面积的求法是一致的，即可求出面积的代数式，求出其最值即可；

（3）由（2）知B在A上方9个单位，所以只需要保证yB＜0就可以了，求解不等式即可．

解：（1）∵y=x2-2mx=，

∴顶点为；

（2）∵直线过抛物线顶点，

∴，

即，

故一次函数解析式为，

联立方程，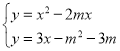

解得，

∵点A的横坐标小于点B的横坐标，

∴将x代入解析式可求得，

∵C(-2，1)，

∴过C点做CD∥y轴交直线于D，

则，

∵，

∴，

，

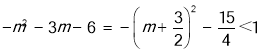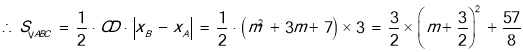∴△ABC面积的最小值为；

（3）由（2）可知，

故使A，B两点都落在x轴的下方只需满足，

解得m＞3或m＜-3，

∴实数m的取值范围为m＞3或m＜-3．