题目内容
【题目】如图,△ABC和△DEF都是等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合。将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,射线EF与线段AB相交于点G,与射线CA相交于点Q.

(1)求证:△BPE∽△CEQ;
(2)求证:DP平分∠BPQ;
【答案】(1)见解析;(2)见解析.
【解析】
(1)由△ABC和△DEF是等腰直角三角形,易得∠B=∠C=∠DEF=45°,然后利用三角形的外角的性质,即可得∠BEP=∠EQC,则可证得△BPE∽△CEQ;
(2)首先证明△BPE∽△EPQ,推出∠BPE=∠EPQ,即可得到∠DPB=∠DPQ,问题得证.
(1)∵△ABC和△DEF是等腰直角三角形,
∴∠B=∠C=∠DEF=45°,
∵∠BEQ=∠EQC+∠C,
即∠BEP+∠DEF=∠EQC+∠C,
∴∠BEP+45°=∠EQC+45°,
∴∠BEP=∠EQC,
∵∠B=∠C=45°,
∴△BPE∽△CEQ,
(2)∵△BPE∽△CEQ,
∴![]() ,
,
∵CE=BE,
∴![]() ,
,
∵∠B=∠DEF=45°,
∴△BPE∽△EPQ,
∴∠BPE=∠EPQ,
∴∠DPB=∠DPQ,
∴DP平分∠BPQ.

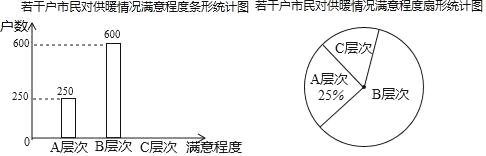
【题目】某综合实践小组为了了解本校学生参加课外读书活动的情况,随机抽取部分学生,调查其最喜欢的图书类别,并根据调查结果绘制成不完整的统计表与统计图,请结合图中的信息解答下列问题.
学生最喜欢的图书类别人数统计表
图书类别 | 画记 | 人数 | 百分比 |
文学类 | |||
艺体类 | 正 | 5 | |
科普类 | 正正一 | 11 | 22% |
其它 | 正正 | 14 | 28% |
合计 | a | 100% |


(1)随机抽取的样本容量a为_________________________;
(2)补全扇形统计图和条形统计图;
(3)已知该校有600名学生,估计全校最喜欢文学类图书的学生人数.