题目内容
已知m为整数,方程2x2+mx-1=0的两个根都大于-1且小于 ,当方程的两个根均为有理数时,求m的值.
,当方程的两个根均为有理数时,求m的值.
【答案】分析:利用二次函数的性质得出当x=-1时,y>0,即:2-m-1>0,进而得出,当x= 时,y>0,即:
时,y>0,即: +
+ m-1>0求出m的取值范围,进而分析得出答案即可.
m-1>0求出m的取值范围,进而分析得出答案即可.
解答:解:设y=2x2+mx-1.
∵2x2+mx-1=0的两根都在-1和 之间,
之间,
∴当x=-1时,y>0,即:2-m-1>0.
当x= 时,y>0,即:
时,y>0,即: +
+ m-1>0.
m-1>0.
∴-2 <m<1.
<m<1.
∵m为整数,
∴m=-2,-1,0;
①当m=-2时,方程2x2-2x-1=0,△=4+8=12,
∴此时方程的根为无理数,不合题意.
②当m=-1时,方程2x2-x-1=0,x1=- ,x2=1,符合题意.
,x2=1,符合题意.
③当m=0时,方程2x2-1=0,x=±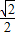 ,不符合题意.
,不符合题意.
综合①②③可知,m=-1.
点评:此题主要考查了一元二次方程的根的分布与系数的关系,解题的关键是理解根的分布与方程相应函数的函数值的对应关系,由此得到参数所满足的不等式,解出符合条件的参数的取值范围.
 时,y>0,即:
时,y>0,即: +
+ m-1>0求出m的取值范围,进而分析得出答案即可.
m-1>0求出m的取值范围,进而分析得出答案即可.解答:解:设y=2x2+mx-1.
∵2x2+mx-1=0的两根都在-1和
 之间,
之间,∴当x=-1时,y>0,即:2-m-1>0.
当x=
 时,y>0,即:
时,y>0,即: +
+ m-1>0.
m-1>0.∴-2
 <m<1.
<m<1.∵m为整数,
∴m=-2,-1,0;
①当m=-2时,方程2x2-2x-1=0,△=4+8=12,
∴此时方程的根为无理数,不合题意.
②当m=-1时,方程2x2-x-1=0,x1=-
 ,x2=1,符合题意.
,x2=1,符合题意.③当m=0时,方程2x2-1=0,x=±
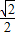 ,不符合题意.
,不符合题意.综合①②③可知,m=-1.
点评:此题主要考查了一元二次方程的根的分布与系数的关系,解题的关键是理解根的分布与方程相应函数的函数值的对应关系,由此得到参数所满足的不等式,解出符合条件的参数的取值范围.

练习册系列答案
相关题目
已知a为整数,关于x的方程a2x-20=0的根是质数,且满足|ax-7|>a2,则a等于( )
| A、2 | B、2或5 | C、土2 | D、-2 |