题目内容
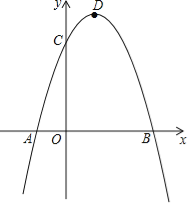
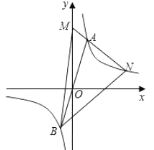
【题目】如图,点![]() 为双曲线
为双曲线![]() 上的一点,连接
上的一点,连接![]() 并延长与双曲线在第三象限交于点
并延长与双曲线在第三象限交于点![]() ,
,![]() 为
为![]() 轴正半轴上一点,连接
轴正半轴上一点,连接![]() 并延长与双曲线交于点
并延长与双曲线交于点![]() ,连接
,连接![]() 、
、![]() ,已知
,已知![]() 的面积为6,则点
的面积为6,则点![]() 的坐标为______.
的坐标为______.
【答案】(![]() ,1)
,1)
【解析】
先求出反比例函数的关系式,设点M、N的坐标,利用双曲线的对称性可求出S△MON=![]() S△BMN,这样可得到关于两点坐标的关系式,联立可求出答案.
S△BMN,这样可得到关于两点坐标的关系式,联立可求出答案.
连接ON,如图:
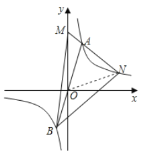
∵点A(1,2)为双曲线![]() 上,
上,
∴![]() ,
,
∴反比例函数的关系式为![]() ,
,
由双曲线的对称性可知:OA=OB,
∴S△MBO=S△MAO,S△NBO=S△NAO,
∴S△MON=![]() S△BMN=3,
S△BMN=3,
设点M(0,m),N(n,![]() ),
),
∴S△MON=![]() ,即
,即![]() ①,
①,
设直线AM的关系式为![]() ,将M(0,m)A(1,2)代入得,
,将M(0,m)A(1,2)代入得,
![]() ,
,
解得:![]() ,
,![]() ,
,
∴直线AM的关系式为![]() ,
,
把N(n,![]() )代入得,
)代入得,![]() ②,
②,
联立①和②解得:![]() (舍去)或
(舍去)或![]() ,
,
当![]() 时,
时,![]() ,
,
∴点N的坐标为(![]() ,1),
,1),
故答案为:(![]() ,1)
,1)

练习册系列答案
相关题目