题目内容
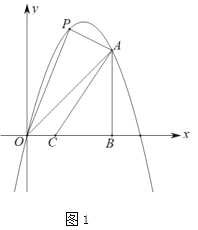
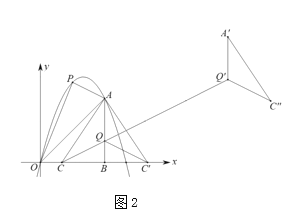
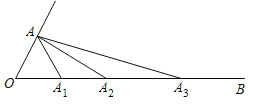
【题目】如图,已知![]() ,点
,点![]() 绕点
绕点![]() 顺时针旋转后的对应点
顺时针旋转后的对应点![]() 落在射线
落在射线![]() 上,点
上,点![]() 绕点
绕点![]() 顺时针旋转后的对应点
顺时针旋转后的对应点![]() 落在射线
落在射线![]() 上,点
上,点![]() 绕点
绕点![]() 顺时针旋转后的对应点
顺时针旋转后的对应点![]() 落在射线
落在射线![]() 上….连接
上….连接![]() ,依此做法,则
,依此做法,则![]() =________,
=________,![]() =________(用含
=________(用含![]() 的代数式表示,
的代数式表示,![]() 为正整数)
为正整数)
【答案】![]()
![]()
【解析】
由点![]() 绕点
绕点![]() 顺时针旋转后的对应点
顺时针旋转后的对应点![]() 落在射线
落在射线![]() 上得到OA=OA1,求出∠AA1O=
上得到OA=OA1,求出∠AA1O=![]() ,由点
,由点![]() 绕点
绕点![]() 顺时针旋转后的对应点
顺时针旋转后的对应点![]() 落在射线
落在射线![]() 上求出∠A1AA2=∠AA2A1=
上求出∠A1AA2=∠AA2A1=![]() ,由点
,由点![]() 绕点
绕点![]() 顺时针旋转后的对应点
顺时针旋转后的对应点![]() 落在射线
落在射线![]() 上求出
上求出![]() ,由此得到规律
,由此得到规律![]() ,再根据邻补角的关系求出
,再根据邻补角的关系求出![]() .
.
∵点![]() 绕点
绕点![]() 顺时针旋转后的对应点
顺时针旋转后的对应点![]() 落在射线
落在射线![]() 上,
上,
∴OA=OA1,
∵![]() ,
,
∴∠AA1O=![]() ,
,
∵点![]() 绕点
绕点![]() 顺时针旋转后的对应点
顺时针旋转后的对应点![]() 落在射线
落在射线![]() 上,
上,
∴A1A=A1A2,
∴∠A1AA2=∠AA2A1=![]() ,
,
∵点![]() 绕点
绕点![]() 顺时针旋转后的对应点
顺时针旋转后的对应点![]() 落在射线
落在射线![]() 上,
上,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() =180°-
=180°-![]() =
=![]() ,
,
故答案为:![]() ,
,![]() .
.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目