Question

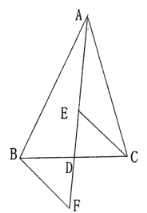
【题目】如图A村和B村在一条大河CD的同侧，它们到河岸的距离AC、BD分别为1千米和4千米，又知道CD的长为4千米.

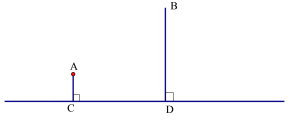
（1）现要在河岸CD上建一水厂向两村输送自来水.有两种方案备选.

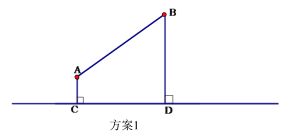
方案1：水厂建在C点，修自来水管道到A村，再到B 村（即AC+AB）.（如图）

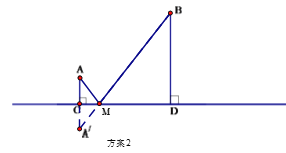
方案2：作A点关于直线CD的对称点，连接交CD 于M点，水厂建在M点处，分别向两村修管道AM和BM. （即AM+BM） （如图）

从节约建设资金方面考虑，将选择管道总长度较短的方案进行施工.请利用已有条件分别进行计算，判断哪种方案更合适.

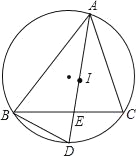
（2）有一艘快艇Q从这条河中驶过，当快艇Q与CD中点G相距多远时，△ABQ为等腰三角形？直接写出答案，不要说明理由.

Answer 1

【答案】（1）方案1更合适；（2）QG=时，△ABQ为等腰三角形.

【解析】

（1）分别求出两种路线的长度进行比较；（2）分类讨论，然后解直角三角形.

（1）过A点作AE⊥BD于E，

∵BD=4，AC=1，

∴BE=3.

∵AE=CD=4，BE=3，

在△ABE中，根据勾股定理得：

AB=，

=5.

过A，作A，H⊥BD于H，

在直角三角形A，HB中，根据勾股定理得：

A，B=，

=，

=，

方案①AC+AB=1+5=6.

方案②AM+MB=A，B=.

∵6＜，

∴方案①路线短，比较合适.

（2）

过A点以AB为半径作圆交CD于E和F点，

图中由勾股定理求得EC=CF=2.所以QG=2-2或2＋2.

过B点为圆心以AB为半径作圆，交CD于G、H.

由勾股定理可求得：GD=DH=3，所以QG=1或5.

做AB的垂直平分线交CD于Q，

求得：QG=.

综上， QG=时，△ABQ为等腰三角形.