题目内容
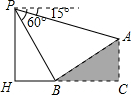
如图,某人在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1: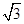 ,点P、H、B、C、A在同一个平面上的点H、B、C在同一条直线上,且PH⊥HC.则A、B两点间的距离是( )
,点P、H、B、C、A在同一个平面上的点H、B、C在同一条直线上,且PH⊥HC.则A、B两点间的距离是( )
A.15 B.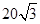 C.
C.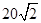 D.
D.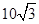
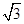 ,点P、H、B、C、A在同一个平面上的点H、B、C在同一条直线上,且PH⊥HC.则A、B两点间的距离是( )
,点P、H、B、C、A在同一个平面上的点H、B、C在同一条直线上,且PH⊥HC.则A、B两点间的距离是( )
A.15 B.
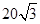 C.
C.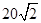 D.
D.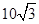
B
由题意可得:∠APB=60°﹣15°=45°,∠PBH=60°,则可由三角函数求得PB的长,又由山坡的坡度i(即tan∠ABC)为1: 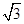 ,即可求得∠ABC的度数,△ABP是等腰直角三角形,则可求得答案.
,即可求得∠ABC的度数,△ABP是等腰直角三角形,则可求得答案.
解:根据题意得:∠APB=60°﹣15°=45°,∠PBH=60°,
∵PH⊥HC,PH=30米,∴PB= =
= =
=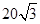 (米),
(米),
∵tan∠ABC= =
= ,
,
∴∠ABC=30°,
∴∠ABP=180°﹣∠PBH﹣∠ABC=180°﹣60°﹣30°=90°,
∴∠PAB=∠APB=45°,
∴AB=PB=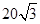 (米).
(米).
即A、B两点间的距离是: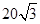 米.
米.
故选B.
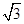 ,即可求得∠ABC的度数,△ABP是等腰直角三角形,则可求得答案.
,即可求得∠ABC的度数,△ABP是等腰直角三角形,则可求得答案.解:根据题意得:∠APB=60°﹣15°=45°,∠PBH=60°,
∵PH⊥HC,PH=30米,∴PB=
 =
= =
=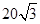 (米),
(米),∵tan∠ABC=
 =
= ,
,∴∠ABC=30°,
∴∠ABP=180°﹣∠PBH﹣∠ABC=180°﹣60°﹣30°=90°,
∴∠PAB=∠APB=45°,
∴AB=PB=
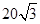 (米).
(米).即A、B两点间的距离是:
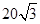 米.
米.故选B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 上确定点D,使CD与
上确定点D,使CD与
 ,
, );
);

 )
)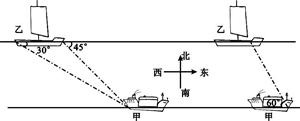
 ≈1.732)
≈1.732)





 |+
|+ =0,则∠C=________.
=0,则∠C=________.