题目内容
4.化简:$\frac{1-{m}^{2}}{1-2m+{m}^{2}}$-$\frac{m-2}{m-1}$.分析 原式通分并利用同分母分式的减法法则计算即可得到结果.
解答 解:原式=$\frac{(1+m)(1-m)}{(m-1)^{2}}$-$\frac{m-2}{m-1}$=-$\frac{m+1}{m-1}$-$\frac{m-2}{m-1}$=-$\frac{2m-1}{m-1}$.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
14.若关于x的一元一次不等式组$\left\{\begin{array}{l}{x-2m<0}\\{x+m>1}\end{array}\right.$有解,则m的取值范围为( )
| A. | m<$\frac{1}{3}$ | B. | m≥$\frac{1}{3}$ | C. | m≤$\frac{1}{3}$ | D. | m>$\frac{1}{3}$ |
12.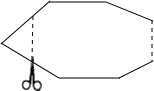 如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2520°的新多边形,则原多边形的边数为( )
如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2520°的新多边形,则原多边形的边数为( )
 如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2520°的新多边形,则原多边形的边数为( )
如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2520°的新多边形,则原多边形的边数为( )| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
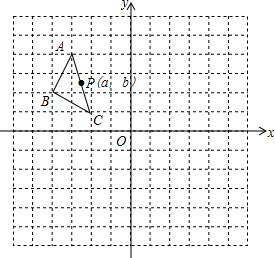 如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(-3,4),B(-4,2),C(-2,1),且△A1B1C1与△ABC关于原点O成中心对称.
如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(-3,4),B(-4,2),C(-2,1),且△A1B1C1与△ABC关于原点O成中心对称.