Question

【题目】已知一次函数y1＝kx+n（n＜0）和反比例函数y2＝（m＞0，x＞0）．

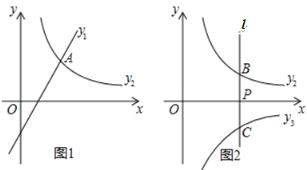
（1）如图1，若n＝﹣2，且函数y1、y2的图象都经过点A（3，4）．

①求m，k的值；

②直接写出当y1＞y2时x的范围；

（2）如图2，过点P（1，0）作y轴的平行线l与函数y2的图象相交于点B，与反比例函数y3＝（x＞0）的图象相交于点C．

①若k＝2，直线l与函数y1的图象相交点D．当点B、C、D中的一点到另外两点的距离相等时，求m﹣n的值；

②过点B作x轴的平行线与函数y1的图象相交于点E．当m﹣n的值取不大于1的任意实数时，点B、C间的距离与点B、E间的距离之和d始终是一个定值．求此时k的值及定值d．

Answer 1

【答案】（1）①m=12；k=2；②x＞3；（2）①m﹣n＝1或4或2；②k＝1，d＝1．

【解析】

（1）①将点A的坐标代入一次函数表达式即可得出k的值，将点A的坐标代入反比例函数表达式即可得出m的值；②由图象可以直接得出结果；
（2）①当x＝1时，点D、B、C的坐标分别为（1，2+n）、（1，m）、（1，n），则BD=|2+n-m|，BC=m-n，DC=2+n-n=2，由BD=BC或BD=DC或BC=CD，即可求解；②先得出点E的坐标为，当点E在点B左侧时，d=BC+BE=m-n+=1+（m-n）（1-），由1-=0即可求解；当点E在点B右侧时，同理BC+BE＝（m﹣n）（1+）﹣1，不合题意舍去．

解：（1）①当n=-2时，一次函数为y1=kx-2，

将点A的坐标（3，4）代入一次函数表达式得，4=3k-2，解得k＝2，

将点A的坐标（3，4）代入反比例函数y2＝得，m＝3×4＝12；

②由图象可以看出x＞3时，y1＞y2；

（2）①由k=2，则y1=2x+n，

当x＝1时，点D、B、C的坐标分别为（1，2+n）、（1，m）、（1，n），

则BD＝|2+n﹣m|，BC＝m﹣n，DC＝2+n﹣n＝2，

则BD＝BC或BD＝DC或BC＝CD，

即：|2+n﹣m|＝m﹣n或|2+n﹣m|＝2或m﹣n＝2，

即：m﹣n＝1或0或2或4，

当m﹣n＝0时，m＝n与题意不符，

点D不能在C的下方，即BC＝CD也不存在，n+2＞n，

当B、D重合时，m﹣n＝2成立，

故m﹣n＝1或4或2；

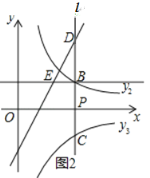
②∵点E的纵坐标与点B的纵坐标相等为m，

y1＝kx+n中令y1=m得，点E的横坐标为，

当点E在点B左侧时，

d＝BC+BE＝m﹣n+（1﹣）＝1+（m﹣n）（1﹣），

m﹣n的值取不大于1的任意数时，d始终是一个定值，

当1﹣＝0时，此时k＝1，从而d＝1．

当点E在点B右侧时，

同理d＝BC+BE＝（m﹣n）（1+）﹣1，

当1+＝0，k＝﹣1时，（不合题意舍去）

故k＝1，d＝1．