题目内容
10.关于x的一元二次方程a(x+2)2+b=0的解是x1=-3,x2=-1,则方程a(x-1)2+b=0的解是x1=0,x2=2.分析 根据一元二次方程a(x+2)2+b=0的解是x1=-3,x2=-1,求出二次函数y=a(x+2)2+b与x轴的交点坐标,从而得出二次函数y=a(x-1)2+b与x轴的交点坐标,即可得出方程a(x-1)2+b=0的解.
解答 解:∵一元二次方程a(x+2)2+b=0的解是x1=-3,x2=-1,
∴二次函数y=a(x+2)2+b与x轴的交点坐标是(-3,0)(-1,0),
∴二次函数y=a(x-1)2+b与x轴的交点坐标是(0,0)(2,0),
∴方程a(x-1)2+b=0的解是x1=0,x2=2,
故答案为:x1=0,x2=2.
点评 此题主要考查了解一元二次方程,用到的知识点是二次函数的移动、二次函数与一元二次方程的关系,关键是掌握一元二次方程的解与二次函数的关系.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
20.在平面直角坐标系中,一次函数y=-3x+1的图象所经过的象限是( )
| A. | 二、三、四 | B. | 一、三、四 | C. | 一、二、四 | D. | 一、二、三 |
20.下面是第五次全国人口普查我国四个直辖市的人口的两幅统计图.由统计图得到的下列结论你认为正确的是( )
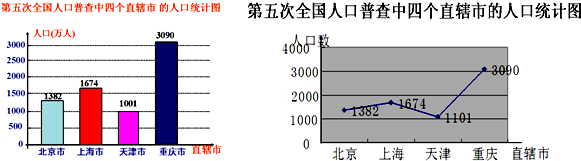

| A. | 重庆的人口与其它三个直辖市人口的和相当 | |
| B. | 重庆的人口增长最快 | |
| C. | 上海相对北京的人口增长的百分数与北京相对天津的人口增长的百分数较小 | |
| D. | 重庆是天津人口总数的3倍还要多 |
 如图,将三角尺直角顶点放在直尺一边上,∠1=30°,∠2=55°,则∠3度数=25°.
如图,将三角尺直角顶点放在直尺一边上,∠1=30°,∠2=55°,则∠3度数=25°.