题目内容

8．若-3＜x＜-2，化简$\sqrt{（x+2）^{2}}$+$\root{3}{（x+3）^{3}}$=1．

分析 根据x的范围判断出x+2的正负，利用二次根式性质及立方根定义计算即可得到结果．

解答 解：∵-3＜x＜-2，
∴x+2＜0，
则原式=|x+2|+x+3=-x-2+x+3=1．
故答案为：1．

点评 此题考查了立方根，以及算术平方根，熟练掌握各自的定义是解本题的关键．

练习册系列答案
相关题目
18．化简
（1）5（a2b-3ab2）-2（a2b-7ab2）；
（2）4x2-[3x-2（x-3）+2（x2-1）]．
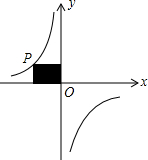19．如图，P是反比例函数y=$\frac{k}{x}$的图象上的一点，过点P分别作x轴、y轴的垂线，得图中阴影部分的面积为6，则这个反比例函数的比例系数是-6．
16．直接写出分解因式的结果：
a2-ab2=a（a-b2），
$4{x^2}-\frac{1}{4}{y^2}$=（2x+$\frac{1}{2}$y）（2x-$\frac{1}{2}$y）；       
a2+6ab+9b2=（a+3b）2；      
4a2+4a+1=（2a+1）2．
3．计算：
（1）$\frac{12xy}{5a}÷6{x^2}y$
（2）$\frac{1}{y-x}+\frac{1}{2y-2x}$
（3）$\frac{12}{{{m^2}-9}}-\frac{2}{m-3}$．
13．求一个数$\sqrt{a^2}$的平方根的运算，叫做开平方；平方与开平方互为逆运算．
20．化简：
（1）$\frac{{x}^{2}}{x-2}$-x-2     
（2）（a-b）2（b-a）2n÷（a-b）2n-1．
17．如图：线段AB=20cm，点C是线段AB上一点，点M是线段BC的中点，点N是线段AB的中点且BM=4cm，求线段NC的长．
18．如图，用一个半径为30cm，面积为300πcm2的扇形铁皮，制作一个无底的圆锥（不计损耗），则圆锥的底面半径r为10cm．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网