题目内容
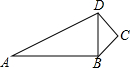如图，∠C=90°，AB=12，BC=3，CD=4，当AD= 时，∠ABD=90°．
- A.10
- B.13
- C.8
- D.11
B
分析：先在直角△BCD中运用勾股定理求出BD=5，然后根据勾股定理的逆定理得出当AD2=AB2+BD2时，∠ABD=90°，由此求出AD的长度．
解答：在直角△BCD中，∵∠C=90°，BC=3，CD=4，
∴BD=5，
在△ABD中，当AD2=AB2+BD2时，∠ABD=90°，
∵AD2=AB2+BD2=122+52=169，
∴AD=13．
故选B．
点评：本题考查了勾股定理及其逆定理，比较简单．在直角△BCD中求出BD=5是解题的关键．
分析：先在直角△BCD中运用勾股定理求出BD=5，然后根据勾股定理的逆定理得出当AD2=AB2+BD2时，∠ABD=90°，由此求出AD的长度．
解答：在直角△BCD中，∵∠C=90°，BC=3，CD=4，
∴BD=5，
在△ABD中，当AD2=AB2+BD2时，∠ABD=90°，
∵AD2=AB2+BD2=122+52=169，
∴AD=13．
故选B．
点评：本题考查了勾股定理及其逆定理，比较简单．在直角△BCD中求出BD=5是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，∠BAC=90°，AD⊥BC，△ABE，△ACF都是等边三角形，则S△ABE：S△ACF等于（ ）| A、AB：AC | B、AD2：DC2 | C、BD2：DC2 | D、AC2：AB2 |
14、如图，∠AOB=90°，∠B=30°，△AOB′可以看作是由△AOB绕点O顺时针旋转α角度得到的，若点A′在AB上，则旋转角α的大小可以是
16、如图，∠C=90°，AD平分∠CAB，DE⊥AB于E，若DB=2DE=6cm，则BC=
已知：如图，∠C=90°，⊙C与AB相交于点D，AC=5，CB=12，求AD．
如图，∠AOB=90°，0C⊥OD，且∠BOC=