题目内容
7.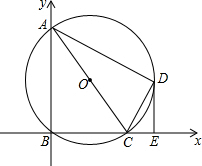 如图,在平面直角坐标系中,点A、C的坐标分别为(0,8)、(6,0),以AC为直径作⊙O,交坐标轴于点B,点D是⊙O 上一点,且弧BD=弧AD,过点D作DE⊥BC,垂足为E.
如图,在平面直角坐标系中,点A、C的坐标分别为(0,8)、(6,0),以AC为直径作⊙O,交坐标轴于点B,点D是⊙O 上一点,且弧BD=弧AD,过点D作DE⊥BC,垂足为E.(1)求证:CD平分∠ACE;
(2)判断直线ED与⊙O的位置关系,并说明理由;
(3)求线段CE的长.
分析 (1)根据四边形ABCD是⊙O内接四边形,可得∠DCE=∠BAD,根据弧BD=弧AD,可得∠BAD=∠ACD,等量代换得到∠DCE=∠ACD,从而求解;
(2)直线ED与⊙O相切.连接OD.根据圆的性质和等边对等角可得∠ODC=∠OCD,等量代换得到∠DCE=∠ODC,根据平行线的判定和性质得到∠ODE=∠DEC,再根据垂直的定义和性质可得OD⊥DE,根据切线的判定即可求解;
(3)延长DO交AB于点H.根据三角形中位线定理可得HO=$\frac{1}{2}$BC=3,根据勾股定理可得OD,得到HD,再根据矩形的判定和性质得到BE=HD=8,从而得到CE的长.
解答 解:(1)∵四边形ABCD是⊙O内接四边形,
∴∠BAD+∠BCD=180°,
又∵∠BCD+∠DCE=180°,
∴∠DCE=∠BAD,
∵弧BD=弧AD,
∴∠BAD=∠ACD, ∴∠DCE=∠ACD,
∴∠DCE=∠ACD,
∴CD平分∠ACE.
(2)直线ED与⊙O相切.
连接OD.
∵OC=OD,
∴∠ODC=∠OCD,
又∵∠DCE=∠ACD,
∴∠DCE=∠ODC,
∵OD∥BE,
∴∠ODE=∠DEC,
又∵DE⊥BC,
∴∠DEC=90°,
∴∠ODE=90°
∴OD⊥DE,
∴ED与⊙O相切.
(3)延长DO交AB于点H.
∵OD∥BE,O是AC的中点,
∴H是AB的中点,
∴HO是△ABC的中位线,
∴HO=$\frac{1}{2}$BC=3,
又∵AC为直径,
∴∠ADC=90°,
又∵O是AC的中点
∴OD=$\frac{1}{2}$AC=$\frac{1}{2}$×$\sqrt{{6}^{2}+{8}^{2}}$=5,
∴HD=3+5=8,
∵∠ABC=∠DEC=∠ODE=90°,
∴四边形BEDH是矩形,
∴BE=HD=8,
∴CE=8-6=2.
点评 考查了圆的综合题,涉及的知识点有:内接四边形的性质,等弧对等角,圆的性质和等边对等角,平行线的判定和性质,垂直的定义和性质,切线的判定,三角形中位线定理,勾股定理,矩形的判定和性质.综合性较强,有一定的难度.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案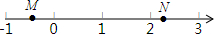 如图,M、N两点在数轴上表示的数分别是m,n,下列式子中成立的是( )
如图,M、N两点在数轴上表示的数分别是m,n,下列式子中成立的是( )| A. | m+n<0 | B. | -m<-n | C. | 2+m>2+n | D. | |m|-|n|>0 |
| A. | 0 | B. | 2 | C. | 4 | D. | 8 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 由n个相同的小正方体组成的几何体,从正面和上面看到的几何体的形状如图所示,则n的最小值是12.
由n个相同的小正方体组成的几何体,从正面和上面看到的几何体的形状如图所示,则n的最小值是12. 已知△ABC在平面直角坐标系中的位置如图所示.
已知△ABC在平面直角坐标系中的位置如图所示.