题目内容
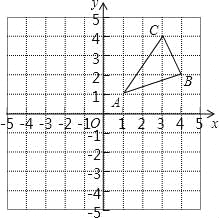
【题目】如图,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.
(1)求点B的坐标;
(2)求经过A、O、B的抛物线的解析式;
(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,请说明理由.
【答案】(1) ![]() . (2)
. (2) ![]() (3)
(3) ![]()
【解析】【试题分析】(1)在直角三角形BCO中利用三角函数求解;(2)知道抛物线与x轴的两个交点,设成交点式求解;(3)抛物线的对称轴是直线x=2,设点P的坐标为(2, y).
分三种情况讨论:①当OP=OB=4时,OP2=16.所以4+y2=16.解得![]() .
.
②当BP=BO=4时,BP2=16.所以![]() .解得
.解得![]() .
.
③当PB=PO时,PB2=PO2.所以![]() .解得
.解得![]() .故求.
.故求.
【试题解析】
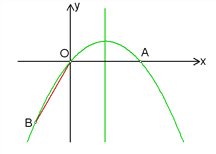
(1)如图1,过点B作BC⊥y轴,垂足为C.
在Rt△OBC中,∠BOC=30°,OB=4,所以BC=2, ![]() .
.
所以点B的坐标为![]() .
.
(2)因为抛物线与x轴交于O、A(4, 0),设抛物线的解析式为y=ax(x-4),
代入点B![]() ,
, ![]() .解得
.解得![]() .
.
所以抛物线的解析式为![]() .
.
(3)抛物线的对称轴是直线x=2,设点P的坐标为(2, y).
①当OP=OB=4时,OP2=16.所以4+y2=16.解得![]() .
.
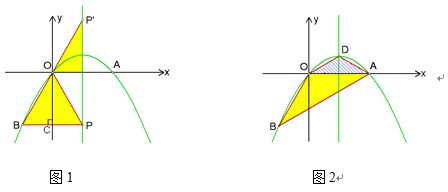
当P在![]() 时,B、O、P三点共线(如图1).
时,B、O、P三点共线(如图1).
②当BP=BO=4时,BP2=16.所以![]() .解得
.解得![]() .
.
③当PB=PO时,PB2=PO2.所以![]() .解得
.解得![]() .
.
综合①、②、③,点P的坐标为![]() ,如图2所示.
,如图2所示.

【题目】某商场销售国外、国内两种品牌的智能手机,这两种手机的进价和售价如表所示
国外品牌 | 国内品牌 | |
进价(万元/部) | 0.44 | 0.2 |
售价(万元/部) | 0.5 | 0.25 |
该商场计划购进两种手机若干部,共需14.8万元,预计全部销售后可获毛利润共2.7万元.[毛利润=(售价﹣进价)×销售量]
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润
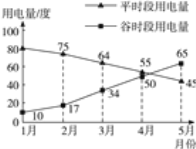
【题目】小明家使用的是分时电表,按平时段(6:00~22:00)和谷时段(22:00~次日6:00)分别计费,平时段每度电价为0.61元,谷时段每度电价为0.30元,小明将家里2012年1月至5月的平时段和谷时段的用电量分别用折线图表示(如下图),同时将前4个月的用电量和相应电费制成表格(如下表).
月用电量(度) | 电费(元) | |
1月 | 90 | 51.80 |
2月 | 92 | 50.85 |
3月 | 98 | 49.24 |
4月 | 105 | 48.55 |
5月 |
根据上述信息,解答下列问题:
(1)计算5月份的用电量和相应电费,将所得结果填入表中;
(2)小明家这5个月的月平均用电量为__________度;
(3)小明家这5个月的月平均用电量呈__________趋势(选择“上升”或“下降”);这5个月每月电费呈__________趋势(选择“上升”或“下降”);
(4)小明预计7月份家中用电量很大,估计7月份用电量可达500度,相应电费将达243元,请你根据小明的估计,计算出7月份小明家平时段用电量和谷时段用电量.