题目内容
如图是一个边长为a的正方形，用代数式表示图中的阴影部分的面积，并求当a=2cm时，阴影部分的面积是多少？（π取3.14，结果保留一位小数）
解：空白部分的面积=a2-
πa2，
∴阴影部分的面积=a2-2（a2-πa2）=
πa2-a2；
∵a=2cm，
∴阴影部分的面积=×3.14×22-22，
=6.28-4，
≈2.3cm2．
分析：先用正方形的面积减扇形的面积求出一个空白部分的面积，再用正方形的面积减去两个空白部分的面积就是阴影部分的面积．
点评：理清根据正方形的面积和扇形的面积先求出空白部分的面积，再用正方形的面积减去空白部分面积的2倍是解题的关键，考查图形的识别能力．
πa2，∴阴影部分的面积=a2-2（a2-
πa2）=πa2-a2；∵a=2cm，
∴阴影部分的面积=
×3.14×22-22，=6.28-4，
≈2.3cm2．
分析：先用正方形的面积减扇形的面积求出一个空白部分的面积，再用正方形的面积减去两个空白部分的面积就是阴影部分的面积．
点评：理清根据正方形的面积和扇形的面积先求出空白部分的面积，再用正方形的面积减去空白部分面积的2倍是解题的关键，考查图形的识别能力．
练习册系列答案
名校课堂系列答案
相关题目
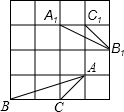如图是一个边长为1的正方形组成的网络，△ABC与△A1B1C1都是格点三角形（顶点在网格交点处），并且△ABC∽△A1B1C1，则△ABC与△A1B1C1的相似比是
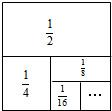
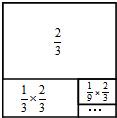
如图是一个边长为a的正方形，用代数式表示图中的阴影部分的面积，并求当a=2cm时，阴影部分的面积是多少？（π取3.14，结果保留一位小数）