题目内容

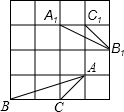精英家教网如图是一个边长为1的正方形组成的网络，△ABC与△A1B1C1都是格点三角形（顶点在网格交点处），并且△ABC∽△A1B1C1，则△ABC与△A1B1C1的相似比是
 
．
分析：先利用勾股定理求出AC，那么AC：A′C′即是相似比．
解答：解：由图可知AC=
12+12
=
2
，A1C1=1，
∴△ABC与△A1B1C1的相似比是
2
：1．
点评：本题考查对相似三角形性质的理解，相似三角形边长的比等于相似比．解答此题的关键是找出相似三角形的对应边．
练习册系列答案
相关题目
如图①是一个边长为1的正方形，顺次连接这个正方形的各边中点得到图②，再顺次连接图②中小正方形各边中点得到图③┉┉依此类推可以得到图④，图⑤等，则图⑨最小的正方形的面积为
 
．
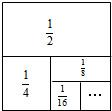
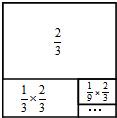
精英家教网
利用图形来表示数量或数量关系，也可以利用数量或数量关系来描述图形特征或图形之间的关系，这种思想方法称为数形结合．我们刚学过的《从面积到乘法公式》就很好地体现了这一思想方法，你能利用数形结合的思想解决下列问题吗？
（1）如图，一个边长为1的正方形，依次取正方形面积的
1
2
、
1
4
、
1
8
、…、
1
2n
，
根据图示我们可以知道：
1
2
+
1
4
+
1
8
+
1
16
+…+
1
2n
=
 
．
精英家教网
利用上述公式计算：2-22-23-24-25-26-…-22008+22009=
 
．
（2）如图，一个边长为1的正方形，依次取剩余部分的
2
3
，根据图示
精英家教网
计算：
2
3
+
2
9
+
2
27
+…+
2
3n
=
 
．
（3）如图是一个边长为1的正方形，根据图示
精英家教网
计算：
1
3
+
2
9
+
4
27
+
8
81
+…+
2n-1
3n
=
 
．
精英家教网如图是一个边长为a的正方形，用代数式表示图中的阴影部分的面积，并求当a=2cm时，阴影部分的面积是多少？（π取3.14，结果保留一位小数）
如图是一个边长为1的正方形组成的网络，△ABC与△A1B1C1都是格点三角形（顶点在网格交点处），并且△ABC∽△A1B1C1，则△ABC与△A1B1C1的相似比是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网