题目内容
8.若2x=4y-1,27y=3x+1,则x-y=-3.分析 根据2x=4y-1,27y=3x+1,可得2x=22y-2,33y=3x+1,所以$\left\{\begin{array}{l}{x=2y-2}\\{3y=x+1}\end{array}\right.$;然后解二元一次方程,求出x、y的值各是多少,进而求出x-y的值是多少即可.
解答 解:∵2x=4y-1,27y=3x+1,
∴2x=22y-2,33y=3x+1,
∴$\left\{\begin{array}{l}{x=2y-2}\\{3y=x+1}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=-4}\\{y=-1}\end{array}\right.$
∴x-y=(-4)-(-1)=-3.
故答案为:-3.
点评 (1)此题主要考查了幂的乘方和积的乘方,要熟练掌握,解答此题的关键是要明确:①(am)n=amn(m,n是正整数);②(ab)n=anbn(n是正整数).
(2)此题还考查了二元一次方程的求解方法,要熟练掌握.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
18.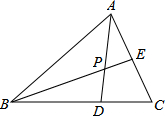 如图,△ABC的面积为3,BD:DC=2:1,E是AC的中点,AD与BE相交于点P,那么四边形PDCE的面积为( )
如图,△ABC的面积为3,BD:DC=2:1,E是AC的中点,AD与BE相交于点P,那么四边形PDCE的面积为( )
 如图,△ABC的面积为3,BD:DC=2:1,E是AC的中点,AD与BE相交于点P,那么四边形PDCE的面积为( )
如图,△ABC的面积为3,BD:DC=2:1,E是AC的中点,AD与BE相交于点P,那么四边形PDCE的面积为( )| A. | $\frac{1}{3}$ | B. | $\frac{7}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{13}{20}$ |
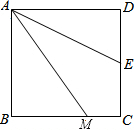 【问题情境】
【问题情境】