题目内容
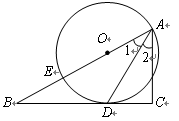
如图，⊙O的直径AB＝4，BC切⊙O于点B，OC平行于弦AD，OC＝5，则AD的长为（ ）
A．
B．
C．
D．
A．
B． C． D．B
连接BD．
∵AB是直径，∴∠ADB=90°．
∵OC∥AD，∴∠A=∠BOC，∴cos∠A=cos∠BOC．
∵BC切⊙O于点B，∴OB⊥BC，
∴cos∠BOC=
，
∴cos∠A=cos∠BOC=
．
又∵cos∠A=
，AB=4，
∴AD=
．
故选B．
∵AB是直径，∴∠ADB=90°．
∵OC∥AD，∴∠A=∠BOC，∴cos∠A=cos∠BOC．
∵BC切⊙O于点B，∴OB⊥BC，
∴cos∠BOC=
，∴cos∠A=cos∠BOC=
．又∵cos∠A=
，AB=4，∴AD=
．故选B．
练习册系列答案
名校课堂系列答案
相关题目
cm
cm
cm
中，
，
，若以
为圆心，
为半径所得的圆与斜边
只有一个公共点，则
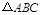中，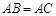
，以AB为直径的
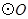交BC
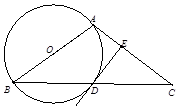
的切线；
的图象交于
、
、
、
四点，已知点
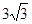，求B E的长．