题目内容
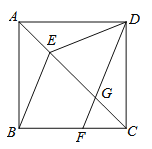
【题目】已知:在![]() 中,
中,![]() ,在
,在![]() 中,
中,![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 和
和![]() .
.
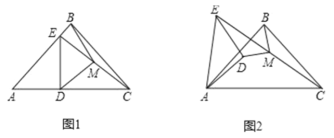
(1)若点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上且与点
上且与点![]() 不重合,如图1,探索
不重合,如图1,探索![]() 的关系并给予证明;
的关系并给予证明;
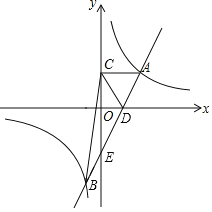
(2)如果将图1中的![]() 绕点
绕点![]() 逆时针旋转小于
逆时针旋转小于![]() 的角,如图2,那么(1)中的结论是否仍成立?如果不成立,请举出反例;如果成立,请给予证明.
的角,如图2,那么(1)中的结论是否仍成立?如果不成立,请举出反例;如果成立,请给予证明.
【答案】(1)![]() ,
,![]() ,见解析;(2)(1)中的结论仍成立,见解析
,见解析;(2)(1)中的结论仍成立,见解析
【解析】
(1)要求BM和DM的关系,可从角的度数入手,由题意,BM是直角三角形CBE斜边上的中线,因此BM=CM,∠MCB=∠MBC,∠BME=2∠MCB,同理可得出∠DME=2∠DCM,根据三角形ABC是个等腰直角三角形,那么∠DCM+∠BCE=45°,因此∠BME+∠DME=2(∠DCM+∠BCM)=90°,由此我们可得出∠BMD=90°,那么BM和DM是互相垂直的;
(2)可通过构建三角形来求解,连接CD和EF,连接BD,延长DM至点F,使得DM=MF,连接BF、FC,延长ED交AC于点H,先证明三角形ADB和CFB全等后,再证明三角形DBF是等腰三角形,即可得出BM⊥DM.
解:(1)![]() ,
,![]() ,
,
在![]() 中,
中,![]() 是斜边
是斜边![]() 的中点,
的中点,
∴![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() 是斜边
是斜边![]() 的中点,
的中点,
∴![]() .
.
∴![]() .
.
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() .
.
(2):(1)中的结论仍成立,
延长![]() 至点
至点![]() ,使得
,使得![]() ,连接
,连接![]() 和
和![]() ,连接
,连接![]() ,连接
,连接![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.
∵![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∵![]()
∵![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() .
.
在![]() 中,由
中,由![]() ,
,![]() ,得
,得![]() 且
且![]() .
.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目