题目内容
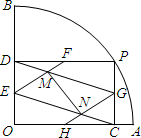 如图,在半径为1的扇形AOB中,∠AOB=90°,点P是
如图,在半径为1的扇形AOB中,∠AOB=90°,点P是 上的一个动点(不与点A、B重合),PC⊥OA,PD⊥OB,垂足分别为点C、D,点E、F、G、H分别是线段OD、PD、PC、OC的中点,EF与DG相交于点M,HG与EC相交于点N,联结MN.如果设OC=x,MN=y,那么y关于x的函数解析式及函数定义域为________.
上的一个动点(不与点A、B重合),PC⊥OA,PD⊥OB,垂足分别为点C、D,点E、F、G、H分别是线段OD、PD、PC、OC的中点,EF与DG相交于点M,HG与EC相交于点N,联结MN.如果设OC=x,MN=y,那么y关于x的函数解析式及函数定义域为________.
y=- x2+
x2+ (o<x<1)
(o<x<1)
分析:建立平面直角坐标系,连接OP交MN于R,交MG于Z,交CE于Q,根据三角形中位线求出EF∥OP∥GH,求出DM=MZ=ZG,EQ=QN=CN,求出E的坐标,即可求出M、N的坐标,根据勾股定理求出MN,即可得出答案.
解答: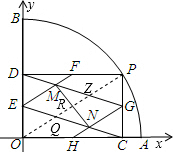
如图,建立平面直角坐标系,连接OP交MN于R,交MG于Z,交CE于Q,
∵点E、F、G、H分别是线段OD、PD、PC、OC的中点,
∴EF∥OP,GH∥OP,
∴DM=MZ,GZ=MZ,
∴DM=MZ=ZG,
同理EQ=QN=CN,
在Rt△OPC中,OC=x,OP=1,由勾股定理得:OD=CP= ,
,
∴E的坐标是(0,
 ),
),
∵CN=NQ=EQ,OC=x,
∴N的横坐标是 OC=
OC= x,N的纵坐标是
x,N的纵坐标是 OE=
OE=
 ,M的横坐标是x-
,M的横坐标是x- x=
x= x,纵坐标是OE-
x,纵坐标是OE-
 =
=

即N( x,
x,
 ),M(
),M( x,
x,
 ),
),
由勾股定理得:MN=( x-
x- x)2+[
x)2+[
 -
-
 )2,
)2,
即y=- x2+
x2+ ,x的范围是:O<x<1.
,x的范围是:O<x<1.
故答案为:y=- x2+
x2+ (0<x<1).
(0<x<1).
点评:本题考查了平行线分线段成比例定理,三角形的中位线,勾股定理等知识点的应用,主要考查学生综合运用性质进行推理和计算的能力,有一定的难度.
 x2+
x2+ (o<x<1)
(o<x<1)分析:建立平面直角坐标系,连接OP交MN于R,交MG于Z,交CE于Q,根据三角形中位线求出EF∥OP∥GH,求出DM=MZ=ZG,EQ=QN=CN,求出E的坐标,即可求出M、N的坐标,根据勾股定理求出MN,即可得出答案.
解答:

如图,建立平面直角坐标系,连接OP交MN于R,交MG于Z,交CE于Q,
∵点E、F、G、H分别是线段OD、PD、PC、OC的中点,
∴EF∥OP,GH∥OP,
∴DM=MZ,GZ=MZ,
∴DM=MZ=ZG,
同理EQ=QN=CN,
在Rt△OPC中,OC=x,OP=1,由勾股定理得:OD=CP=
 ,
,∴E的坐标是(0,

 ),
),∵CN=NQ=EQ,OC=x,
∴N的横坐标是
 OC=
OC= x,N的纵坐标是
x,N的纵坐标是 OE=
OE=
 ,M的横坐标是x-
,M的横坐标是x- x=
x= x,纵坐标是OE-
x,纵坐标是OE-
 =
=

即N(
 x,
x,
 ),M(
),M( x,
x,
 ),
),由勾股定理得:MN=(
 x-
x- x)2+[
x)2+[
 -
-
 )2,
)2,即y=-
 x2+
x2+ ,x的范围是:O<x<1.
,x的范围是:O<x<1.故答案为:y=-
 x2+
x2+ (0<x<1).
(0<x<1).点评:本题考查了平行线分线段成比例定理,三角形的中位线,勾股定理等知识点的应用,主要考查学生综合运用性质进行推理和计算的能力,有一定的难度.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目

 如图,在一块四边形场地的四个角修建四个半径为2米的扇花台,那么四个花台的总面积是
如图,在一块四边形场地的四个角修建四个半径为2米的扇花台,那么四个花台的总面积是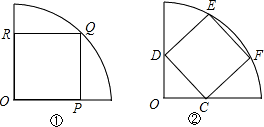

 如图,在一块四边形场地的四个角修建四个半径为2米的扇花台,那么四个花台的总面积是________平方米(结果中保留π).
如图,在一块四边形场地的四个角修建四个半径为2米的扇花台,那么四个花台的总面积是________平方米(结果中保留π).