题目内容
已知2m2-5m-1=0,| 1 |
| n2 |
| 5 |
| n |
| 1 |
| m |
| 1 |
| n |
分析:根据已知条件求得n+m=
,然后利用完全平方和公式求得mn=-
;最后代入所求解答即可.
| 5 |
| 2 |
| 1 |
| 2 |
解答:解:∵
+
-2=0,
∴2n2-5n-1=0,①
∵2m2-5m-1=0,②
由①-②,得
2(n-m)(n+m)-5(n-m)=0,
∵m≠n,
∴2(n+m)=5,即n+m=
;
由①+②,得
2(n2+m2)-5(n+m)-2=0,即2(n2+m2)-5×
-2=0,
解得,n2+m2=
,
∴mn=[(m+n)2-(n2+m2)]÷2=-
,
∴
+
=
=-5.
故答案为-5.
| 1 |
| n2 |
| 5 |
| n |
∴2n2-5n-1=0,①
∵2m2-5m-1=0,②
由①-②,得
2(n-m)(n+m)-5(n-m)=0,
∵m≠n,
∴2(n+m)=5,即n+m=
| 5 |
| 2 |
由①+②,得
2(n2+m2)-5(n+m)-2=0,即2(n2+m2)-5×
| 5 |
| 2 |
解得,n2+m2=
| 29 |
| 4 |
∴mn=[(m+n)2-(n2+m2)]÷2=-
| 1 |
| 2 |
∴
| 1 |
| m |
| 1 |
| n |
| m+n |
| mn |
故答案为-5.
点评:本题考查了代数式的求值.解答此题时,利用完全平方和公式求得mn=-
.注意,在求代数式
+
的值时,要先通分,后代入数值.
| 1 |
| 2 |
| 1 |
| m |
| 1 |
| n |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的值.
的值. ,所以1-q-q2 =0可变形为:(
,所以1-q-q2 =0可变形为:( 的值
的值 )2+
)2+ -2=0,且m≠n ,求
-2=0,且m≠n ,求 的值.
的值. ,且m≠n,则
,且m≠n,则 的值是________.
的值是________. 的值。
的值。 )2-(
)2-( )-1=0 ,
)-1=0 ,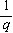 )2-(
)2-(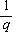 )-1=0的特征,
)-1=0的特征, 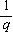 =1
=1 =1
=1  ,且m≠n ,求
,且m≠n ,求 +
+ 的值。
的值。