Question

17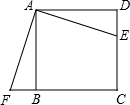．如图，点E是正方形ABCD的边CD上一点，点F是正方形ABCD的边CB的延长线上一点，连接AF，且△ADE绕点A沿顺时针方向旋转一定角度能与△ABF重合．
（1）请你连结EF，判定△AEF的形状，并说明理由；
（2）若正方形ABCD的周长为24，DE：CD=1：3，求点B到AF的距离．

Answer 1

分析 （1）根据正方形的性质得AB=AD，∠BAD=90°再根据旋转的性质得AE=AF，∠EAF=∠BAD=90°，于是可判断△AEF为等腰直角三角形；
（2）作BH⊥AF于H，如图，先计算出AB=AD=CD=6，DE=$\frac{1}{3}$CD=2，再利用勾股定理计算出AE=2$\sqrt{10}$，根据旋转的性质得BF=DE=2，AF=AE=2$\sqrt{10}$，然后利用面积法计算出BH即可．

解答 解：（1）△AEF为等腰直角三角形．理由如下：
∵四边形ABCD为正方形，
∴AB=AD，∠BAD=90°，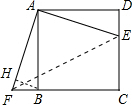
∵△ADE绕点A沿顺时针方向旋转一定角度能与△ABF重合，
∴AE=AF，∠EAF=∠BAD=90°，
∴△AEF为等腰直角三角形；
（2）作BH⊥AF于H，如图，
∵正方形ABCD的周长为24，
∴AB=AD=CD=6，
∵DE：CD=1：3，
∴DE=$\frac{1}{3}$CD=2，
∴AE=$\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$，
∵△ADE绕点A沿顺时针方向旋转90°得到△ABF，
∴BF=DE=2，AF=AE=2$\sqrt{10}$，
∴BH=$\frac{2×6}{2\sqrt{10}}$=$\frac{3\sqrt{10}}{5}$，
即点B到AF的距离为$\frac{3\sqrt{10}}{5}$．

点评 本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了正方形的性质和等腰直角三角形的判定．