题目内容
已知关于x的方程x2+ax+a-2=0,若该方程的一个根为1,则a= ,该方程的另一根为 .
考点:一元二次方程的解,根与系数的关系
专题:
分析:设方程的另一个根为x,则由根与系数的关系得:x+1=-a,x•1=a-2,求出即可.
解答:解:设方程的另一个根为x,
则由根与系数的关系得:x+1=-a,x•1=a-2,
解得:x=-
,a=
,
即a=
,方程的另一个根为-
.
故答案为:
,-
.
则由根与系数的关系得:x+1=-a,x•1=a-2,
解得:x=-
| 3 |
| 2 |
| 1 |
| 2 |
即a=
| 1 |
| 2 |
| 3 |
| 2 |
故答案为:
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查了根与系数关系的关系的应用,注意:如果x1,x2是一元二次方程ax2+bx+c=0(a、b、c为常数,a≠0)的两个根,则x1+x2=-
,x1•x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
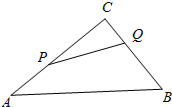 如图,△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从点A开始沿AC向点C以2厘米/秒的速度运动;与此同时,点Q从点C开始沿CB边向点B以1厘米/秒的速度运动;如果P、Q分别从A、C同时出发,当其中一点到达终点时,另一点也随之停止运动.
如图,△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从点A开始沿AC向点C以2厘米/秒的速度运动;与此同时,点Q从点C开始沿CB边向点B以1厘米/秒的速度运动;如果P、Q分别从A、C同时出发,当其中一点到达终点时,另一点也随之停止运动. 如图,AB=AC,AD⊥BC,点C在AE的垂直平分线上,DE=6,则△ABC的周长为
如图,AB=AC,AD⊥BC,点C在AE的垂直平分线上,DE=6,则△ABC的周长为 如图,已知,在△ABC中,CD交AB于点E,AE:EB=1:3,EF∥BC∥AD,EF交AC于点F,S△ADE=a.求S△BCE和S△AEF的值.
如图,已知,在△ABC中,CD交AB于点E,AE:EB=1:3,EF∥BC∥AD,EF交AC于点F,S△ADE=a.求S△BCE和S△AEF的值.