题目内容
如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E,交PC于点F,连接AF.
(1)判断AF与⊙O的位置关系并说明理由;
(2)若⊙O的半径为4,AF=3,求AE的长.(2013舟山卷改编)
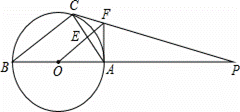
(1)AF为圆O的切线,理由为:
 连接OC,
连接OC,
 ∵PC为圆O切线,
∵PC为圆O切线,
 ∴CP⊥OC,
∴CP⊥OC,
 ∴∠OCP=90°,
∴∠OCP=90°,
 ∵OF∥BC,
∵OF∥BC,
 ∴∠AOF=∠B,∠COF=∠OCB, 2分
∴∠AOF=∠B,∠COF=∠OCB, 2分
 ∵OC=OB,
∵OC=OB,
 ∴∠OCB=∠B,
∴∠OCB=∠B,
 ∴∠AOF=∠COF,
∴∠AOF=∠COF,
 由△AOF≌△COF得,
由△AOF≌△COF得,
 ∴∠OAF=∠OCF=90°,
∴∠OAF=∠OCF=90°,
 则AF为圆O的切线; 4分
则AF为圆O的切线; 4分

 (2)∵△AOF≌△COF,
(2)∵△AOF≌△COF,
 ∴∠AOF=∠COF,
∴∠AOF=∠COF,
 ∵OA=OC,
∵OA=OC,
 ∴E为AC中点,即AE=CE=
∴E为AC中点,即AE=CE= AC,OE⊥AC,
AC,OE⊥AC,
 ∵OA⊥AF, 6分
∵OA⊥AF, 6分
 ∴在Rt△AOF中,OA=4,AF=3,
∴在Rt△AOF中,OA=4,AF=3,
 根据勾股定理得:OF=5,
根据勾股定理得:OF=5,
 ∵S△AOF=
∵S△AOF= •OA•AF=
•OA•AF= •OF•AE,
•OF•AE,
 ∴AE=
∴AE= , 8分
, 8分

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目

 ,使点
,使点 落在
落在 边上的点
边上的点 ,且折痕
,且折痕 ,若
,若 ,
, ,则
,则 的度数为____________.
的度数为____________.
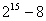 可以被在60~70之间的两个整数整除,则这两个数是63、65;
可以被在60~70之间的两个整数整除,则这两个数是63、65;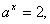
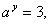 则
则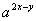 =
=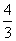 ;
;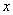 的方程
的方程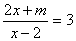 的解是正数,则m的取值范围为
的解是正数,则m的取值范围为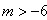 ;
;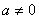 ),则方程a(x+m+2)2+b=0的解是____________.
),则方程a(x+m+2)2+b=0的解是____________.  D.-
D.- 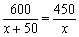 B.
B.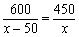
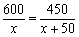 D.
D.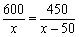
 C. 0 D.一l
C. 0 D.一l