题目内容
18．在Rt△ABC中，∠C=90°．（1）已知 c=15，∠B=36°，求∠A的度数和a，b的长；
（2）已知 a=24，∠A=80°，求∠B的度数和b，c的长．
分析 （1）先利用直角三角形两锐角互余计算出∠A的度数，再利用∠A的正弦计算a的值，然后利用∠B的正弦计算b的值；
（2）先利用直角三角形两锐角互余计算出∠B的度数，再利用∠A的正弦计算c的值，然后利用∠B的正切计算b的值．
解答 解：（1）∵∠B=36°，
∴∠A=90°-∠B=54°；
∵sinA=$\frac{a}{c}$，
∴a=15×sin54°≈12.1；
∵sinB=$\frac{b}{c}$，
∴b=15×sin36°≈8.8；
（2）∵∠A=80°，
∴∠B=90°-∠A=10°；
∵sinA=$\frac{a}{c}$，
∴c=$\frac{24}{sin80°}$≈24.4；
∵tanB=$\frac{b}{a}$，
∴b=24•tan10°≈4.2．
点评 本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．解直角三角形要用到的关系（Rt△ABC中，∠C=90°，a、b、c分别是∠A、∠B、∠C的对边）：
①两锐角之间的关系：∠A+∠B=90°；
②三边之间的关系：a2+b2=c2；
③边角之间的关系：sinA=∠A的对边：斜边=a：c，cosA=∠A的邻边：斜边=b：c，tanA=∠A的对边：∠A的邻边=a：b．
练习册系列答案
步步高达标卷系列答案
相关题目
8．在将式子$\frac{m}{\sqrt{m}}$（m＞0）化简时，
小明的方法是：$\frac{m}{\sqrt{m}}=\frac{m•\sqrt{m}}{\sqrt{m•}\sqrt{m}}=\frac{m\sqrt{m}}{m}=\sqrt{m}$；
小亮的方法是：$\frac{m}{\sqrt{m}}=\frac{（\sqrt{m}）^{2}}{\sqrt{m}}=\sqrt{m}$；
小丽的方法是：$\frac{m}{\sqrt{m}}=\frac{\sqrt{{m}^{2}}}{\sqrt{m}}=\sqrt{\frac{{m}^{2}}{m}}=\sqrt{m}$．
则下列说法正确的是（ ）
小明的方法是：$\frac{m}{\sqrt{m}}=\frac{m•\sqrt{m}}{\sqrt{m•}\sqrt{m}}=\frac{m\sqrt{m}}{m}=\sqrt{m}$；
小亮的方法是：$\frac{m}{\sqrt{m}}=\frac{（\sqrt{m}）^{2}}{\sqrt{m}}=\sqrt{m}$；
小丽的方法是：$\frac{m}{\sqrt{m}}=\frac{\sqrt{{m}^{2}}}{\sqrt{m}}=\sqrt{\frac{{m}^{2}}{m}}=\sqrt{m}$．
则下列说法正确的是（ ）
| A． | 小明、小亮的方法正确，小丽的方法不正确 | |
| B． | 小明、小丽的方法正确，小亮的方法不正确 | |
| C． | 小明、小亮、小丽的方法都正确 | |
| D． | 小明、小丽、小亮的方法都不正确 |
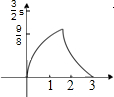
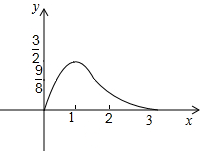
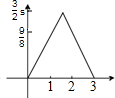
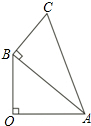两直角△如图放置，∠AOB=∠ABC=90°，OA=OB=3，点C到OA、OB的距离分别为4，1．将△OAB沿射线OA方向移m个单位（0＜m＜3），得到新△O1A1B1与△ABC重叠部分的面积记为S，则能表示S与m的函数关系如图象是（ ）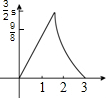
已知△ABC内切圆O于点D、E、F，延长CO交EF于M，延长BO交EF于G，证明．S△BOC=S四边形AMOG．