题目内容
 如图,AB∥CD,EG⊥AB,垂直为G,若∠1=54°,则∠E的度数是________.
如图,AB∥CD,EG⊥AB,垂直为G,若∠1=54°,则∠E的度数是________.
36°
分析:由AB∥CD,根据两直线平行,同位角相等,即可求得∠AMC的度数,然后根据对顶角相等与直角三角形中两锐角互余,即可求得∠E的度数.
解答: 解:∵AB∥CD,
解:∵AB∥CD,
∴∠AMG=∠1=54°,
∴∠EMG=∠AMC=54°,
∵EG⊥AB,
∴∠EGM=90°,
∴∠E=90°-∠EMG=36°.
故答案为:36°.
点评:此题考查了平行线的性质、对顶角相等,以及直角三角形的性质.此题比较简单,解题的关键是注意掌握两直线平行,同位角相等定理的应用,注意数形结合思想的应用.
分析:由AB∥CD,根据两直线平行,同位角相等,即可求得∠AMC的度数,然后根据对顶角相等与直角三角形中两锐角互余,即可求得∠E的度数.
解答:
 解:∵AB∥CD,
解:∵AB∥CD,∴∠AMG=∠1=54°,
∴∠EMG=∠AMC=54°,
∵EG⊥AB,
∴∠EGM=90°,
∴∠E=90°-∠EMG=36°.
故答案为:36°.
点评:此题考查了平行线的性质、对顶角相等,以及直角三角形的性质.此题比较简单,解题的关键是注意掌握两直线平行,同位角相等定理的应用,注意数形结合思想的应用.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
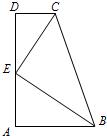 23、如图,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点.求证:CE⊥BE.
23、如图,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点.求证:CE⊥BE.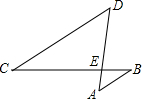 如图,AB∥CD,AD与BC相交于点E,如果AB=2,CD=6,AE=1,那么DE=
如图,AB∥CD,AD与BC相交于点E,如果AB=2,CD=6,AE=1,那么DE=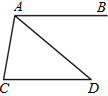 4、如图,AB∥CD,∠C=80°,∠CAD=60°,则∠BAD的度数等于( )
4、如图,AB∥CD,∠C=80°,∠CAD=60°,则∠BAD的度数等于( ) 34、如图,AB∥CD,P是BC上的一个动点,设∠CDP=∠1,∠CPD=∠2,请你猜想出∠1、∠2与∠B之间的关系,并说明理由.
34、如图,AB∥CD,P是BC上的一个动点,设∠CDP=∠1,∠CPD=∠2,请你猜想出∠1、∠2与∠B之间的关系,并说明理由. 如图,AB∥CD,∠1=58°,则∠2的度数是( )
如图,AB∥CD,∠1=58°,则∠2的度数是( )