题目内容
如图，AB与CD相交于E，且AE=8，BE=12，CE=4，若△AEC与△DEB相似，则ED=________．
6
分析：根据相似三角形的性质：相似三角形的对应边成比例，来求ED的值．
解答：∵△AEC∽△DEB，
∴
=
；
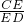又AE=8，BE=12，CE=4，
∴ED=6；
故答案为：6．
点评：本题考查对相似三角形性质的理解．
（1）相似三角形周长的比等于相似比；
（2）相似三角形面积的比等于相似比的平方；
（3）相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比．
分析：根据相似三角形的性质：相似三角形的对应边成比例，来求ED的值．
解答：∵△AEC∽△DEB，
∴
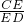=；又AE=8，BE=12，CE=4，
∴ED=6；
故答案为：6．
点评：本题考查对相似三角形性质的理解．
（1）相似三角形周长的比等于相似比；
（2）相似三角形面积的比等于相似比的平方；
（3）相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比．
练习册系列答案
相关题目
如图，AB与CD相交于E，AE=EB，CE=ED，D为线段FB的中点，CF与AB交于点G，若CF=15cm，求GF之长．
已知：如图，AB与CD相交于点O，∠ACO=∠BDO，OC=OD，CE是△ACO的角平分线．请你先作△ODB的角平分线DF（用尺规作图，不要求写出作法与证明，但要保留作图痕迹）；再证明CE=DF．
如图，AB与CD相交于点O，OA=3，OB=5，0D=6．当OC=
如图，AB与CD相交于点E，AE=CE，如果根据“SAS”可以判定△ADE≌△CBE，那么只需要补充一个条件
如图，AB与CD相交于O点，∠1=50°，则∠2=