题目内容
用适当的方法解方程:
①(2x-1)2=9;
②4x2-8x+1=0(配方法);
③2x-1)2=9(1-2x);
④3x2+5(2x+1)=1.
解:①∵(2x-1)2=9,
∴2x-1=±3,
即2x-1=3或2x-1=-3,
解得:x1=2,x2=-1;
②∵4x2-8x+1=0,
∴4x2-8x=-1,
∴x2-2x=- ,
,
∴x2-2x+1=- +1,
+1,
∴(x-1)2= ,
,
解得:x1=1+ ,x2=1-
,x2=1- ;
;
③∵(2x-1)2=9(1-2x),
∴(2x-1)2+9(2x-1)=0,
∴(2x-1)(2x-1+9)=0,
即2x-1=0或2x-1+9=0,
解得:x1= ,x2=-4;
,x2=-4;
④∵3x2+5(2x+1)=1,
∴3x2+10x+4=0,
∴a=3,b=10,c=4,
∴△=b2-4ac=52,
∴x= =
=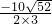 =
=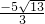 ,
,
解得:x1=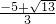 ,x2=
,x2=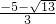 .
.
分析:(1)利用直接开平方法的方法求解即可求得答案;
(2)利用配方法:先移项,再把二次项系数化为1,然后配方求解即可求得答案;
(3)利用因式分解法,提取公因式(2x-1),即可求得答案;
(4)首先整理,然后利用公式法求解即可求得答案.
点评:此题考查了一元二次方程的解法.此题难度不大,解题的关键是选择适当的解题方法.
∴2x-1=±3,
即2x-1=3或2x-1=-3,
解得:x1=2,x2=-1;
②∵4x2-8x+1=0,
∴4x2-8x=-1,
∴x2-2x=-
 ,
,∴x2-2x+1=-
 +1,
+1,∴(x-1)2=
 ,
,解得:x1=1+
 ,x2=1-
,x2=1- ;
;③∵(2x-1)2=9(1-2x),
∴(2x-1)2+9(2x-1)=0,
∴(2x-1)(2x-1+9)=0,
即2x-1=0或2x-1+9=0,
解得:x1=
 ,x2=-4;
,x2=-4;④∵3x2+5(2x+1)=1,
∴3x2+10x+4=0,
∴a=3,b=10,c=4,
∴△=b2-4ac=52,
∴x=
 =
=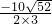 =
=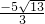 ,
,解得:x1=
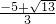 ,x2=
,x2=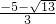 .
.分析:(1)利用直接开平方法的方法求解即可求得答案;
(2)利用配方法:先移项,再把二次项系数化为1,然后配方求解即可求得答案;
(3)利用因式分解法,提取公因式(2x-1),即可求得答案;
(4)首先整理,然后利用公式法求解即可求得答案.
点评:此题考查了一元二次方程的解法.此题难度不大,解题的关键是选择适当的解题方法.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目