题目内容
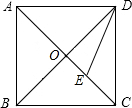
如图所示，正方形ABCD的对角线相交于点O，点E是BC上任意一点，EG⊥BD于G，EF⊥AC于F，若AC=10，则EG+EF的值为
- A.10
- B.4
- C.8
- D.5
D
试题分析：根据ABCD是正方形，求得△BEG，△CEF是等腰直角三角形，即可求得结果。
∵ABCD是正方形，AC，BD是对角线，
∴∠OBC=∠OCB=45°，
∵EG⊥BD，EF⊥AC，
∴△BEG，△CEF是等腰直角三角形．
∴CF=EF．
∵AC⊥BD，
∴EFOG是矩形．
∴EG=FO．
∴EF+EG=CF+FO=CO=5，
故选D.
考点：本题考查了正方形的性质，等腰直角三角形的性质
点评：解答本题的关键是根据ABCD是正方形，求得△BEG，△CEF是等腰直角三角形．
试题分析：根据ABCD是正方形，求得△BEG，△CEF是等腰直角三角形，即可求得结果。
∵ABCD是正方形，AC，BD是对角线，
∴∠OBC=∠OCB=45°，
∵EG⊥BD，EF⊥AC，
∴△BEG，△CEF是等腰直角三角形．
∴CF=EF．
∵AC⊥BD，
∴EFOG是矩形．
∴EG=FO．
∴EF+EG=CF+FO=CO=5，
故选D.
考点：本题考查了正方形的性质，等腰直角三角形的性质
点评：解答本题的关键是根据ABCD是正方形，求得△BEG，△CEF是等腰直角三角形．
练习册系列答案
相关题目
4、如图所示，正方形ABCD中，E，F是对角线AC上两点，连接BE，BF，DE，DF，则添加下列哪一个条件可以判定四边形BEDF是菱形（ ）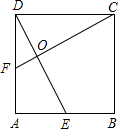
如图所示，正方形ABCD中，E为AB中点，F为AD中点，DE、CF交于O点，求证：DE⊥CF．
如图所示，正方形ABCD的对角线AC，BD相交于点O，DE平分∠ODC交OC于点E，若AB=2，则线段OE的长为（ ）A、
| ||||
B、
| ||||
C、2-
| ||||
D、
|
如图所示，正方形ABCD的边长为1，点E为AB的中点，以E为圆心，1为半径作圆，分别交AD，BC于M，N两点，与DC切于点P，则图中阴影部分面积是
如图所示的正方形网格中（网格中的每个小正方形边长是1），△ABC的顶点均在格点上，请在所给的直角坐标系中解答下列问题：