Question

【题目】已知抛物线C：，直线l：y=kx（k＞0），当k=1时，抛物线C与直线l只有一个公共点．

（1）求m的值；

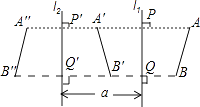
（2）若直线l与抛物线C交于不同的两点A，B，直线l与直线l1：y=﹣3x+b交于点P，且，求b的值；

（3）在（2）的条件下，设直线l1与y轴交于点Q，问：是否在实数k使S△APQ=S△BPQ？若存在，求k的值，若不存在，说明理由．

Answer 1

【答案】（1）4；（2）8；（3）不存在．

【解析】

试题分析：（1）两图象有一个交点，则对应的方程组有一组解，即△=0，代入计算即可求出m的值；

（2）作出辅助线，得到△OAC∽△OPD，+=2，同理+=2，AC，BE是x2﹣（k+3）x+4=0两根，即可；

（3）由S△APQ=S△BPQ得到AC+BE=2PD，建立方程（k+3）2=16即可．

试题解析：（1）当k=1时，抛物线C与直线l只有一个公共点，∴直线l解析式为y=x，∵，∴，∴，∴△=16﹣4m=0，∴m=4；

（2）如图，分别过点A，P，B作y轴的垂线，垂足依次为C，D，E，则△OAC∽△OPD，∴．

同理，．

∵，∴，∴，∴，即．

解方程组：，得x=，即PD=．

由方程组消去y，得．

∵AC，BE是以上一元二次方程的两根，∴AC+BE=k+3，AC×BE=4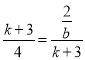，∴．解得b=8．

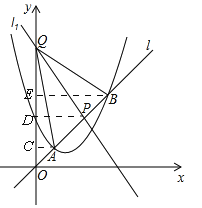
（3）不存在．理由如下：

假设存在，当S△APQ=S△BPQ时，有AP=PB，于是PD﹣AC=PE﹣PD，即AC+BE=2PD．

由（2）可知AC+BE=k+3，PD=，∴k+3=2×，即．

解得k=1（舍去k=﹣7）．

当k=1时，A，B两点重合，△BQA不存在，∴不存在实数k使S△APQ=S△BPQ．