题目内容
5．
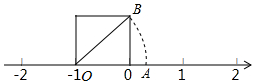如图所示，认真观察，探讨下列问题：（1）如图，OA=OB，数轴上A点对应的数表示什么？
（2）在图中的数轴上作出表示$-\sqrt{5}$的点．
分析 根据勾股定理，可得OB的长；根据勾股定理，可得OB的长，根据圆的性质，可得OC的长．
解答 解：（1）由勾股定理得，
OB=$\sqrt{{1}^{2}{+1}^{2}}$=$\sqrt{2}$，
由圆的半径相等，得
OA=OB=$\sqrt{2}$；
数轴上点A对应的数是$\sqrt{2}$；
（2）如图，
由勾股定理得，
OB=$\sqrt{{2}^{2}{+1}^{2}}$=$\sqrt{5}$，
由圆的半径相等，得
OC=OB=$\sqrt{5}$；
数轴上点C对应的数是-$\sqrt{5}$．
点评 本题考查了实数与数轴、勾股定理，利用勾股定理是解答此题的关键．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
15．数1425万平方米，用科学记数法表示为（ ）平方米．
| A． | 1.425×108 | B． | 1.425×107 | C． | 14.25×106 | D． | 1425×104 |
13．三角形三个内角的度数比是1：2：3，它们的最大边的长等于16，则最小边的长为（ ）
| A． | 4 | B． | 2 | C． | 8 | D． | 6 |
10．张华记录了今年雨季钱塘江一周内水位变化的情况如下表（正号表示比前一天高，负号表示比前一天低）：
（1）本周星期二水位最高，星期日水位最低．
（2）与上周末相比，本周日的水位是上升了还是下降了？（写出计算过程）
（2）请用折线统计图表示钱塘江一周内水位变化的情况．
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 水位变化（m） | +0.25 | +0.80 | -0.40 | +0.03 | +0.28 | -0.36 | -0.04 |
（2）与上周末相比，本周日的水位是上升了还是下降了？（写出计算过程）
（2）请用折线统计图表示钱塘江一周内水位变化的情况．
14．王老师自驾轿车沿高速公路从A地到B地旅游，途经两座跨海大桥，共用了4.5小时；返回时平均速度提高了10千米/小时，比去时少用了半小时回到A地．
（1）求A、B两地间的路程．
（2）两座跨海大桥的长度及过桥费见表．
该省交通部门规定：轿车的高速公路通行费y（元）的计算方法为：y=ax+b+5，其中a（元/千米）为高速公路里程费，x（千米）为高速公路里程（不包括跨海大桥长），b（元）为跨海大桥过桥费．若王老师从A地到B地所花的高速公路通行费为295.4元，求轿车的高速公路里程费a．
（1）求A、B两地间的路程．
（2）两座跨海大桥的长度及过桥费见表．
| 大桥名称 | 跨海大桥1 | 跨海大桥2 |
| 大桥长度 | 48千米 | 36千米 |
| 过桥费 | 100元 | 80元 |
