题目内容
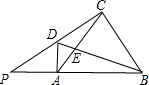 如图,在△PBC中,∠PCB=90゜,DA⊥PB于A点,连AC,BD相交于E点.
如图,在△PBC中,∠PCB=90゜,DA⊥PB于A点,连AC,BD相交于E点.求证:
(1)△PAD∽△PCB;
(2)∠PCA=∠PBD;
(3)△ADE∽△BCE.
分析:(1)利用垂直的定义以及两角对应相等两三角形相似即可得出;
(2)利用△PAD∽△PCB,得出
=
,进而利用两边对应比值相等,且夹角相等两三角形相似进而得出即可;
(3)利用(2)中所证得出∠ADB=∠ECB,进而得出相似.
(2)利用△PAD∽△PCB,得出
| PA |
| CP |
| PD |
| AB |
(3)利用(2)中所证得出∠ADB=∠ECB,进而得出相似.
解答:证明:(1)∵∠PCB=90゜,DA⊥PB,
∴∠PAD=∠PCB,
又∵∠P=∠P,
∴△PAD∽△PCB;
(2)∵△PAD∽△PCB,
∴
=
,
∵∠P=∠P,
∴△CPA∽△BPD,
∴∠PCA=∠PBD;
(3)∵∠ADB+∠ABD=90°,∠PCA+∠ACB=90°,
∠PCA=∠PBD;
∴∠ADB=∠ECB,
又∵∠DEA=∠CEB,
∴△ADE∽△BCE.

∴∠PAD=∠PCB,
又∵∠P=∠P,
∴△PAD∽△PCB;
(2)∵△PAD∽△PCB,
∴
| PA |
| CP |
| PD |
| AB |
∵∠P=∠P,
∴△CPA∽△BPD,
∴∠PCA=∠PBD;
(3)∵∠ADB+∠ABD=90°,∠PCA+∠ACB=90°,
∠PCA=∠PBD;
∴∠ADB=∠ECB,
又∵∠DEA=∠CEB,
∴△ADE∽△BCE.
点评:此题主要考查了相似三角形的判定与性质,熟练掌握相似三角形的判定方法是解题关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
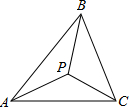 如图,在△ABC中,点P是△ABC的内心,则∠PBC+∠PCA+∠PAB的度数为( )
如图,在△ABC中,点P是△ABC的内心,则∠PBC+∠PCA+∠PAB的度数为( )| A、150° | B、120° | C、90° | D、60° |
 18、(1)如图,在△PAB中AB边上方求作一点C,使AC=BC;
18、(1)如图,在△PAB中AB边上方求作一点C,使AC=BC; 如图,在△ABC中,AB=AC,P为△ABC内一点,且∠BAP=70°,∠ABP=40°,
如图,在△ABC中,AB=AC,P为△ABC内一点,且∠BAP=70°,∠ABP=40°, 如图,在△PBC中,∠PCB=90゜,DA⊥PB于A点,连AC,BD相交于E点.
如图,在△PBC中,∠PCB=90゜,DA⊥PB于A点,连AC,BD相交于E点.