题目内容
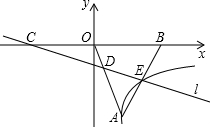
如图,△AOB为等边三角形,点B的坐标为(-2,0),过点C(2,0)作直线l交AO于D,交AB于E, 点E在某反比例函数图象上,当△ADE和△DCO的面积相等时,那么该反比例函数解析式为
点E在某反比例函数图象上,当△ADE和△DCO的面积相等时,那么该反比例函数解析式为分析:根据等边三角形的性质和勾股定理求得AE的长,再求出点E的坐标,从而求出k值,得出解析式.
解答: 解:连接AC.
解:连接AC.
∵点B的坐标为(-2,0),△AOB为等边三角形,
∵AO=OC=2,
∴∠OCA=∠OAC,
∵∠AOB=60°,
∴∠ACO=30°,∠B=60°,
∴∠BAC=90°,
∴点A的坐标为(-1,
),
∵S△ADE=S△DCO,S△AEC=S△ADE+S△ADC,S△AOC=S△DCO+S△ADC,
∴S△AEC=S△AOC=
×AE•AC=
•CO•
,
即
•AE•2
=
×2×
,
∴AE=1.
∴E点为AB的中点(-
,
)
把E点(-
,
)代入y=
k=-
.
所以反比例函数解析式为y=-
=-
.
 解:连接AC.
解:连接AC.∵点B的坐标为(-2,0),△AOB为等边三角形,
∵AO=OC=2,
∴∠OCA=∠OAC,
∵∠AOB=60°,
∴∠ACO=30°,∠B=60°,
∴∠BAC=90°,
∴点A的坐标为(-1,
| 3 |
∵S△ADE=S△DCO,S△AEC=S△ADE+S△ADC,S△AOC=S△DCO+S△ADC,
∴S△AEC=S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
即
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
∴AE=1.
∴E点为AB的中点(-
| 3 |
| 2 |
| ||
| 2 |
把E点(-
| 3 |
| 2 |
| ||
| 2 |
| k |
| x |
k=-
3
| ||
| 4 |
所以反比例函数解析式为y=-
| ||||
| x |
3
| ||
| 4x |
点评:主要考查了用待定系数法求反比例函数的解析式.先设y=
,再把已知点的坐标代入可求出k值,即得到反比例函数的解析式.主要考查了用待定系数法求反比例函数的解析式和反比例函数系数k的几何意义.先设y=
再根据k的几何意义求出k值即可.反比例函数系数k的几何意义为:反比例函数图象上的点的横纵坐标之积是定值k,同时|k|也是该点到两坐标轴的垂线段与两坐标轴围成的矩形面积.本题综合性强,考查知识面广,能较全面考查学生综合应用知识的能力.
| k |
| x |
| k |
| x |

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
 (2013•湖州一模)如图,△AOB为等边三角形,点A在第四象限,点B的坐标为(4,0),过点C(-4,0)作直线l交AO于D,交AB于E,且点E在某反比例函数x图象上,当△ADE和△DCO的面积相等时,k的值为( )
(2013•湖州一模)如图,△AOB为等边三角形,点A在第四象限,点B的坐标为(4,0),过点C(-4,0)作直线l交AO于D,交AB于E,且点E在某反比例函数x图象上,当△ADE和△DCO的面积相等时,k的值为( )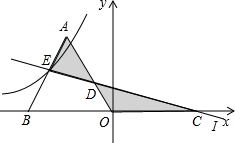 (2012•上虞市模拟)如图,△AOB为等边三角形,点B的坐标为(-2,0),过点C(2,0)作直线l交AO于点D,交AB于E,点E在反比例函数
(2012•上虞市模拟)如图,△AOB为等边三角形,点B的坐标为(-2,0),过点C(2,0)作直线l交AO于点D,交AB于E,点E在反比例函数 (2013•普陀区模拟)如图,△AOB为等边三角形,点B的坐标为(-2,0),过点C(2,0)作直线l交AO于点D,交AB于E,点E在反比例函数
(2013•普陀区模拟)如图,△AOB为等边三角形,点B的坐标为(-2,0),过点C(2,0)作直线l交AO于点D,交AB于E,点E在反比例函数 如图,△AOB为等边三角形,点B的坐标为(-2,0),过点C(2,0)作直线l交AO于D,交AB于E,点E在某反比例函数图象上,当△ADE和△DCO的面积相等时,那么该反比例函数解析式为( )
如图,△AOB为等边三角形,点B的坐标为(-2,0),过点C(2,0)作直线l交AO于D,交AB于E,点E在某反比例函数图象上,当△ADE和△DCO的面积相等时,那么该反比例函数解析式为( )