Question

（2013•普陀区模拟）如图，△AOB为等边三角形，点B的坐标为（-2，0），过点C（2，0）作直线l交AO于点D，交AB于E，点E在反比例函数y=

k

x

(x＜0）的图象上，若△ADE和△DCO（即图中两阴影部分）的面积相等，则k值为（　　）

• A．-

  2

  2

• B．-

  3

  2

• C．-

  2

  4

• D．-

  3 3

  4

Answer 1

分析：连接AC，先由等边三角形及等腰三角形的性质判断出△ABC是直角三角形，再由S_△ADE=S_△DCO，S_△AEC=S_△ADE+S_△ADC，S_△AOC=S_△DCO+S_△ADC，可得出S_△AEC=S_△AOC，故可得出AE的长，再由中点坐标公式求出E点坐标，把点E代入反比例函数y=

k

x

即可求出k的值．

解答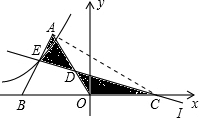：解：连接AC．
∵点B的坐标为（-2，0），△AOB为等边三角形，
∵AO=OC=2，
∴∠OCA=∠OAC，
∵∠AOB=60°，
∴∠ACO=30°，∠B=60°，
∴∠BAC=90°，
∴点A的坐标为（-1，

3

），
∵S_△ADE=S_△DCO，S_△AEC=S_△ADE+S_△ADC，S_△AOC=S_△DCO+S_△ADC，
∴S_△AEC=S_△AOC=

1

2

×AE•AC=

1

2

×CO×

3

，
即

1

2

AE•2

3

=

1

2

×2×

3

，
∴AE=1．
∴E点为AB的中点（-

3

2

，

3

2

）
把E点（-

3

2

，

3

2

）代入y=

k

x

得，k=（-

3

2

）×

3

2

=-

3 3

4

．
故答案为：-

3 3

4

．

点评：本题考查的是反比例函数综合题，涉及到直角三角形的判定与性质、等边三角形的性质、三角形的面积等有关知识，综合性较强．