题目内容
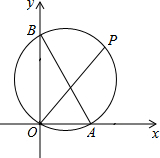 如图,已知A、B两点的坐标分别为(2,0)、(0,4),P是△AOB外接圆⊙C上的一点,且∠AOP=45°,则点P的坐标为
如图,已知A、B两点的坐标分别为(2,0)、(0,4),P是△AOB外接圆⊙C上的一点,且∠AOP=45°,则点P的坐标为考点:全等三角形的判定与性质,角平分线的性质,圆心角、弧、弦的关系,圆周角定理
专题:计算题
分析:由OA与OB的长,利用勾股定理求出AB的长,根据∠AOP=45°,得到三角形OPE为等腰直角三角形,即P横纵坐标相等,设为P(a,a),由∠AOB为直角,利用直角所对的弦为直径得到AB为直径,Rt△AOB外接圆的圆心为AB中点,求出圆心C坐标,过点C作CF∥OA,过点P作PE⊥OA于E交CF于F,在直角三角形PCF中,利用勾股定理列出关于a的方程,求出方程的解得到a的值,确定出P的坐标即可.
解答: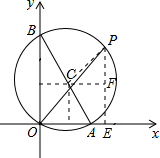 解:∵OB=4,OA=2,
解:∵OB=4,OA=2,
∴AB=
=2
,
∵∠AOP=45°,
∴P点横纵坐标相等,可设为a,即P(a,a),
∵∠AOB=90°,
∴AB是直径,
∴Rt△AOB外接圆的圆心为AB中点,坐标C(1,2),
P点在圆上,P点到圆心的距离为圆的半径
.
过点C作CF∥OA,过点P作PE⊥OA于E交CF于F,
∴∠CFP=90°,
∴PF=a-2,CF=a-1,PC=
,
∴根据勾股定理得:(a-2)2+(a-1)2=(
)2,
解得:a=3,
∴P(3,3);
故答案为:(3,3).
 解:∵OB=4,OA=2,
解:∵OB=4,OA=2,∴AB=
| OA2+OB2 |
| 5 |
∵∠AOP=45°,
∴P点横纵坐标相等,可设为a,即P(a,a),
∵∠AOB=90°,
∴AB是直径,
∴Rt△AOB外接圆的圆心为AB中点,坐标C(1,2),
P点在圆上,P点到圆心的距离为圆的半径
| 5 |
过点C作CF∥OA,过点P作PE⊥OA于E交CF于F,
∴∠CFP=90°,
∴PF=a-2,CF=a-1,PC=
| 5 |
∴根据勾股定理得:(a-2)2+(a-1)2=(
| 5 |
解得:a=3,
∴P(3,3);
故答案为:(3,3).
点评:此题考查了全等三角形的判定与性质,圆周角定理,勾股定理,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
下列方程中,属于一元二次方程的是( )
| A、x+y=2 | ||
| B、x2-2y+1=0 | ||
C、2y2-
| ||
D、
|
化简-a
的结果是( )
-
|
A、
| ||
B、
| ||
C、-
| ||
D、-
|
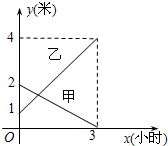 自来水公司有甲、乙两个长方体的蓄水池,现将甲池中的水以每小时8m3的速度注入乙池,则两水池中水的高度y(m)与注水的时间x(h)之间的函数图象如图所示.若要乙池的蓄水量是甲池的2倍,则注水的时间应为( )
自来水公司有甲、乙两个长方体的蓄水池,现将甲池中的水以每小时8m3的速度注入乙池,则两水池中水的高度y(m)与注水的时间x(h)之间的函数图象如图所示.若要乙池的蓄水量是甲池的2倍,则注水的时间应为( )| A、2h | ||
B、
| ||
C、
| ||
D、
|
 某几何体的三视图如图所示,则这个几何体是( )
某几何体的三视图如图所示,则这个几何体是( )A、 |
B、 |
C、 |
D、 |
 如图,△ABC在平面直角坐标系,点A(0,
如图,△ABC在平面直角坐标系,点A(0,