题目内容
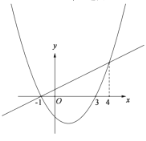
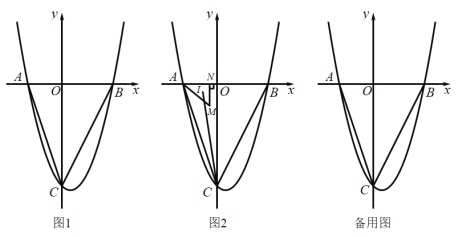
【题目】如图1,抛物线![]() 与x轴交于A、B两点,与y轴交于C点,连接
与x轴交于A、B两点,与y轴交于C点,连接![]() 、
、![]() ,已知点A、C的坐标为
,已知点A、C的坐标为![]() 、
、![]() .
.
(1)求抛物线的表达式;
(2)点P是线段![]() 下方抛物线上的一动点,如果在x轴上存在点Q,使得以点B、C、P、Q为顶点的四边形为平行四边形,求点Q的坐标;
下方抛物线上的一动点,如果在x轴上存在点Q,使得以点B、C、P、Q为顶点的四边形为平行四边形,求点Q的坐标;
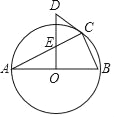
(3)如图2,若点M是![]() 内一动点,且满足
内一动点,且满足![]() ,过点M作
,过点M作![]() ,垂足为N,设
,垂足为N,设![]() 的内心为I,试求
的内心为I,试求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)Q的坐标为
;(2)Q的坐标为![]() 或
或![]() ;(3)
;(3)![]() 的最小值为
的最小值为![]()
【解析】
(1)待定系数法求解析式;
(2)根据![]() 即点C坐标,可以求出P点坐标,算出CP长,即可写出Q点坐标;
即点C坐标,可以求出P点坐标,算出CP长,即可写出Q点坐标;
(3)利用![]() 可判断出I的运动轨迹是圆弧,设I运动轨迹所在的圆心为G
可判断出I的运动轨迹是圆弧,设I运动轨迹所在的圆心为G
计算出圆心G的坐标及半径为,当G、I、C三点共线时候![]() 最短.
最短.
(1)由题意得:A点坐标为![]() ,C点坐标为
,C点坐标为![]() 带入
带入![]() 中
中
得:![]() ,
,
解得:![]()
∴抛物线的解析式为![]() .
.
(2)∵点Q在x轴上,又点B、C、P、Q为顶点的四边形是平行四边形
∴![]() ,由对称性可知,P点的坐标为
,由对称性可知,P点的坐标为![]()
∴![]() ,∴
,∴![]() .
.
∴Q的坐标为![]() 或
或![]() .
.
(3)连接![]() ,
,![]() ,
,![]()

∵I为![]() 的内心
的内心
∴![]() 、
、![]() 分别平分
分别平分![]() ,
,![]()
∴![]()
又∵![]() ,∴
,∴![]()
∴![]() .
.
又∵![]() ,
,![]()
∴![]()
∴![]()
∴I的运动轨迹是圆弧.
设I运动轨迹所在的圆心为G
∵![]() ,∴
,∴![]()
又∵![]() ,
,![]()
∴圆心G的坐标为![]() ,半径为
,半径为![]()
当G、I、C三点共线时候![]() 最短
最短
∵![]() ,
,![]()
∴![]() 的最小值为
的最小值为![]()
综上所述:![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
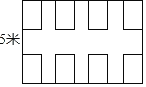
【题目】如图所示的是一个宽5米的餐厅,只能放8张餐桌.现计划扩建增加座位,只能对原宽度进行加长,设加长后的长度为m米.若餐厅的餐桌数为y,经计算,得到如下数据:(注:m和y都为正整数)
m(米) | 5 | 8 | 11 | 14 | …… |
餐桌数y(张) | 8 | 12 | 16 | …… |
(1)根据表中数据的规律,完成以上表格;
(2)求出y关于m的函数解析式;
(3)若这家餐厅至少要有80张餐桌,求m的最小值.