题目内容
【题目】抛物线![]() 与
与![]() 轴的公共点是
轴的公共点是![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,直线
,直线![]() 与抛物线
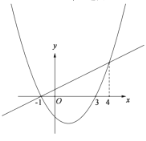
与抛物线![]() 另一个交点的横坐标是4,它们的图象如图所示,有以下结论:
另一个交点的横坐标是4,它们的图象如图所示,有以下结论:
①拋物线对称轴是![]() ;
;
②![]() ;
;
③![]() 时,
时,![]() ;
;
④若![]() ,则
,则![]() .
.
其中正确的个数为( )
A.1B.2C.3D.4
【答案】D
【解析】
利用抛物线的对称性即可求出抛物线的对称轴,从而判断①;将![]() 代入抛物线的解析式中,即可判断②;结合图象即可判断③;利用待定系数法求出二次函数解析式,从而求出一次函数和二次函数图象的交点坐标,然后利用待定系数法求出一次函数解析式即可判断④.
代入抛物线的解析式中,即可判断②;结合图象即可判断③;利用待定系数法求出二次函数解析式,从而求出一次函数和二次函数图象的交点坐标,然后利用待定系数法求出一次函数解析式即可判断④.
解:∵抛物线![]() 与
与![]() 轴的公共点是
轴的公共点是![]() ,
,![]() ,
,
∴拋物线对称轴是![]() ,故①正确;
,故①正确;
将![]() 代入抛物线的解析式中,得
代入抛物线的解析式中,得![]() ,故②正确;
,故②正确;
由图象可知:当![]() 时,
时,![]() ,故③正确;
,故③正确;
∵![]()
∴抛物线的解析式为![]()
将![]() ,
,![]() 代入解析式中,得
代入解析式中,得

解得:
∴抛物线的解析式为![]()
当x=4时,y=![]()
将![]() 和(4,
和(4,![]() )代入
)代入![]() 中,得
中,得

解得: ,故④正确.
,故④正确.
综上:正确的个数为4
故选D.

练习册系列答案
相关题目