题目内容
 如图,直线y=kx(k>0)与双曲线y=
如图,直线y=kx(k>0)与双曲线y= 交于A,B两点,若A,B两点的坐标分别为A(x1,y1),B(x2,y2),则x1y2+x2y1的值为
交于A,B两点,若A,B两点的坐标分别为A(x1,y1),B(x2,y2),则x1y2+x2y1的值为
- A.-8
- B.4
- C.-4
- D.0
C
分析:根据直线y=kx(k>0)与双曲线y= 两交点A,B关于原点对称,求出y1=-y2,y2=-y1,代入解析式即可解答.
两交点A,B关于原点对称,求出y1=-y2,y2=-y1,代入解析式即可解答.
解答:将y= 化为xy=2,将A(x1,y1),B(x2,y2)分别代入xy=2,得x1y1=2,x2y2=2.
化为xy=2,将A(x1,y1),B(x2,y2)分别代入xy=2,得x1y1=2,x2y2=2.
因为y1和y2互为相反数,所以y1=-y2,y2=-y1.则x1y2+x2y1=-x1y1-x2y2=-(x1y1+x2y2)=-(2+2)=-4.
故选C.
点评:此题考查了反比例函数图象的对称性,同学们要熟记才能灵活运用.
分析:根据直线y=kx(k>0)与双曲线y=
 两交点A,B关于原点对称,求出y1=-y2,y2=-y1,代入解析式即可解答.
两交点A,B关于原点对称,求出y1=-y2,y2=-y1,代入解析式即可解答.解答:将y=
 化为xy=2,将A(x1,y1),B(x2,y2)分别代入xy=2,得x1y1=2,x2y2=2.
化为xy=2,将A(x1,y1),B(x2,y2)分别代入xy=2,得x1y1=2,x2y2=2.因为y1和y2互为相反数,所以y1=-y2,y2=-y1.则x1y2+x2y1=-x1y1-x2y2=-(x1y1+x2y2)=-(2+2)=-4.
故选C.
点评:此题考查了反比例函数图象的对称性,同学们要熟记才能灵活运用.

练习册系列答案
相关题目
 如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )
如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )| A、3 | ||
B、
| ||
C、
| ||
D、-
|
 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式| 1 |
| 2 |
| A、x<2 |
| B、x>-1 |
| C、x<1或x>2 |
| D、-1<x<2 |
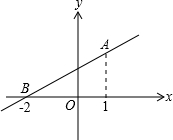 如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为
如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为 7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( )
7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( ) 16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为
16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为