题目内容
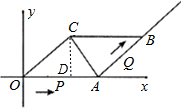
已知,在平行四边形OABC中,OA=5,AB=4,∠OCA=90°,动点P从O点出发沿射线OA方向 以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.
以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.
(1)求直线AC的解析式;
(2)试求出当t为何值时,△OAC与△PAQ相似?
(3)若⊙P的半径为
,⊙Q的半径为
;当⊙P与对角线AC相切时,判断⊙Q与直线AC、BC的位置关系,并求出Q点坐标.
 以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.
以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.(1)求直线AC的解析式;
(2)试求出当t为何值时,△OAC与△PAQ相似?
(3)若⊙P的半径为
| 8 |
| 5 |
| 3 |
| 2 |
(1)过C点作x轴的垂线,垂足为D点,在平行四边形OABC中,由OA=5,AB=4,∠OCA=90°,得AC=3,
由面积法,得CD×OA=OC×AC,解得CD=
=
,
在Rt△OCD中,由勾股定理得OD=
=
,
∴C(
,
),
又∵A(5,0),
∴直线AC解析式为:y=-
x+
;
(2)当0≤t≤2.5时,P在OA上,若∠OAQ=90°时,
故此时△OAC与△PAQ不可能相似.
当t>2.5时,
①若∠APQ=90°,则△APQ∽△OAC,
故
=
=
,
∴
=
,
∴t=
,
∵t>2.5,
∴t=
符合条件.
②若∠AQP=90°,则△APQ∽△OAC,
故
=
=
,
∴
=
,
∴t=
,
∵t>2.5,
∴t=
符合条件.
综上可知,当t=
或
时,△OAC与△APQ相似.
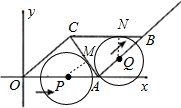 (3)⊙Q与直线AC、BC均相切.
(3)⊙Q与直线AC、BC均相切.
如图,设⊙P与AC相切于点M,则PM∥OC,
∴
=
,即
×5=PA×4,
解得PA=2,OP=5-2=3,
P点运动时间为3÷2=
秒,
故Q点运动时间为
秒,此时AQ=
,
BQ=4-
=
,
过Q点作QN⊥BC,垂足为N,则△BQN∽△BCA,
=
,即
=
,
解得QN=
,
则AQ=QN,
∵AC⊥AB,
∴⊙Q与直线AC、BC均相切.
此时,Q点坐标为(
,
).
由面积法,得CD×OA=OC×AC,解得CD=
| 4×3 |
| 5 |
| 12 |
| 5 |
在Rt△OCD中,由勾股定理得OD=
| OC2-CD2 |
| 16 |
| 5 |
∴C(
| 16 |
| 5 |
| 12 |
| 5 |
又∵A(5,0),
∴直线AC解析式为:y=-
| 4 |
| 3 |
| 20 |
| 3 |

(2)当0≤t≤2.5时,P在OA上,若∠OAQ=90°时,
故此时△OAC与△PAQ不可能相似.
当t>2.5时,
①若∠APQ=90°,则△APQ∽△OAC,
故
| AQ |
| AP |
| OC |
| OA |
| 4 |
| 5 |
∴
| 2t-5 |
| t |
| 4 |
| 5 |
∴t=
| 25 |
| 6 |
∵t>2.5,
∴t=
| 25 |
| 6 |
②若∠AQP=90°,则△APQ∽△OAC,
故
| AQ |
| AP |
| OC |
| OA |
| 4 |
| 5 |
∴
| t |
| 2t-5 |
| 4 |
| 5 |
∴t=
| 20 |
| 3 |
∵t>2.5,
∴t=
| 20 |
| 3 |
综上可知,当t=
| 25 |
| 6 |
| 20 |
| 3 |
 (3)⊙Q与直线AC、BC均相切.
(3)⊙Q与直线AC、BC均相切.如图,设⊙P与AC相切于点M,则PM∥OC,
∴
| PM |
| OC |
| PA |
| OA |
| 8 |
| 5 |
解得PA=2,OP=5-2=3,
P点运动时间为3÷2=
| 3 |
| 2 |
故Q点运动时间为
| 3 |
| 2 |
| 3 |
| 2 |
BQ=4-
| 3 |
| 2 |
| 5 |
| 2 |
过Q点作QN⊥BC,垂足为N,则△BQN∽△BCA,
| QN |
| QB |
| AC |
| BC |
| QN | ||
|
| 3 |
| 5 |
解得QN=
| 3 |
| 2 |
则AQ=QN,
∵AC⊥AB,
∴⊙Q与直线AC、BC均相切.
此时,Q点坐标为(
| 31 |
| 5 |
| 9 |
| 10 |

练习册系列答案
相关题目
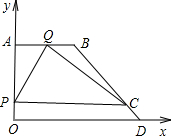 点Q也随之停止运动.
点Q也随之停止运动.





