题目内容
如图,在平面直角坐标系中,已知点A(0,16),D(24,0),点B在第一象限,且AB∥x轴,BD=20,动点P从原点O开始沿y轴正半轴以每秒4个单位长的速度向点A匀速运动,过点P作x轴的平行线与BD交于点C;动点Q从点A开始沿线段AB-BD以每秒8个单位长的速度向点D匀速运动,设点P、Q同时开始运动且时间为t(t>0),当点P与点A重合时停止运动,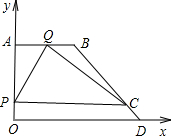 点Q也随之停止运动.
点Q也随之停止运动.
(1)求点B的坐标及BD所在直线的解析式;
(2)当t为何值时,点Q和点C重合?
(3)当点Q在AB上(包括点B)运动时,求S△PQC与t的函数关系式;
(4)若∠PQC=90°时,求t的值.
 点Q也随之停止运动.
点Q也随之停止运动.(1)求点B的坐标及BD所在直线的解析式;
(2)当t为何值时,点Q和点C重合?
(3)当点Q在AB上(包括点B)运动时,求S△PQC与t的函数关系式;
(4)若∠PQC=90°时,求t的值.
(1)∵A(0,16),D(24,0)
∴AO=16,OD=24
过点B作BF⊥OD于F,
∴∠BOF=90°,AO∥BF,且AB∥x轴
∴四边形ABFO是矩形
∴BF=AO=16
在Rt△BFD中,由勾股定理,得
FD=12
∴OF=12
∴B(12,16)
设直线BD的解析式为y=kx+b,由题意,得
,解得
∴直线BD的解析式为y=-
x+32
(2)∵PC∥OD
∴
=
∴
=
∴EC=12-3t
∴PC=24-3t,BE=16-4t
过点Q作QH⊥OD于H,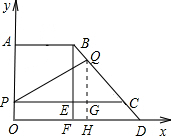
∴
=
∵BQ=8t-12
∴DQ=32-8t
∴
=
,解得
QH=
∴GQ=
∴
=0,解得
t1=8(不符合题意),t2=
∴当t2=
时点Q和点C重合.
(3)当0<t≤1.5时
S△PQC=
∴S△PQC=6t2-72t+192
∴当点Q在AB上(包括点B)运动时,求S△PQC与t的函数关系式为S△PQC=6t2-72t+192
(4)∵
=
∴
=
∴DC=5t
∴CQ=32-13t
∵∠PQC=90°
∴△BFD∽△PQC
∴
=
∴
=
,
解得t=

∴AO=16,OD=24
过点B作BF⊥OD于F,
∴∠BOF=90°,AO∥BF,且AB∥x轴
∴四边形ABFO是矩形
∴BF=AO=16
在Rt△BFD中,由勾股定理,得
FD=12
∴OF=12
∴B(12,16)
设直线BD的解析式为y=kx+b,由题意,得
|
|
∴直线BD的解析式为y=-
| 4 |
| 3 |
(2)∵PC∥OD
∴
| EC |
| FD |
| BE |
| BF |
∴
| EC |
| 12 |
| 16-4t |
| 16 |
∴EC=12-3t
∴PC=24-3t,BE=16-4t
过点Q作QH⊥OD于H,

∴
| DQ |
| BD |
| QH |
| BF |
∵BQ=8t-12
∴DQ=32-8t
∴
| 32-8t |
| 20 |
| QH |
| 16 |
QH=
| 108-32t |
| 5 |
∴GQ=
| 108-52t |
| 5 |
∴
| ||
| 2 |
t1=8(不符合题意),t2=
| 27 |
| 13 |
∴当t2=
| 27 |
| 13 |
(3)当0<t≤1.5时
S△PQC=
| (24-3t)(16-4t) |
| 2 |
∴S△PQC=6t2-72t+192
∴当点Q在AB上(包括点B)运动时,求S△PQC与t的函数关系式为S△PQC=6t2-72t+192
(4)∵
| BE |
| BF |
| BC |
| BD |
∴
| 20-DC |
| 20 |
| 16-4t |
| 16 |
∴DC=5t
∴CQ=32-13t
∵∠PQC=90°
∴△BFD∽△PQC
∴
| FD |
| CQ |
| BD |
| PC |
∴
| 12 |
| 32-13t |
| 20 |
| 24-3t |
解得t=
| 11 |
| 7 |


练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目

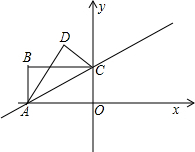
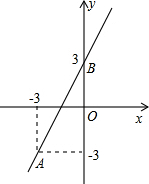
 以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.
以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.

 司的月费用为y2元,y1,y2分别与x之间的函数关系的图象(两条射线)如图所示,观察图象回答下列问题:
司的月费用为y2元,y1,y2分别与x之间的函数关系的图象(两条射线)如图所示,观察图象回答下列问题: 我们就称直线l1与直线l2互相平行.解答下面的问题:
我们就称直线l1与直线l2互相平行.解答下面的问题: